2025年综合应用创新题典中点九年级数学下册鲁教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年综合应用创新题典中点九年级数学下册鲁教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 下列式子中,是二次根式的是 ( )
A. $\sqrt{6}$
B. $5^{2}$
C. 5
D. $\frac{2}{5}$
A. $\sqrt{6}$
B. $5^{2}$
C. 5
D. $\frac{2}{5}$
答案:
A
2. 下列二次根式中,是最简二次根式的是( )
A. $\sqrt{8x}$
B. $\sqrt{y^{2}-4}$
C. $\sqrt{\frac{1}{m}}$
D. $\sqrt{3a^{2}}$
A. $\sqrt{8x}$
B. $\sqrt{y^{2}-4}$
C. $\sqrt{\frac{1}{m}}$
D. $\sqrt{3a^{2}}$
答案:
B
3. 下列计算正确的是 ( )
A. $4\div4\sqrt{2}=\sqrt{2}$
B. $3\times\sqrt{\frac{1}{3}}=\sqrt{3}$
C. $\sqrt{5^{2}-3^{2}}=5 - 3 = 2$
D. $\sqrt{\frac{-9}{-16}}=\frac{\sqrt{-9}}{\sqrt{-16}}=\frac{-3}{-4}=\frac{3}{4}$
A. $4\div4\sqrt{2}=\sqrt{2}$
B. $3\times\sqrt{\frac{1}{3}}=\sqrt{3}$
C. $\sqrt{5^{2}-3^{2}}=5 - 3 = 2$
D. $\sqrt{\frac{-9}{-16}}=\frac{\sqrt{-9}}{\sqrt{-16}}=\frac{-3}{-4}=\frac{3}{4}$
答案:
C
4. [2024·菏泽期末]若代数式$\frac{x}{\sqrt{x + 1}}$在实数范围内有意义,则实数$x$的取值范围是 ( )
A. $x\geq - 1$且$x\neq0$
B. $x>1$
C. $x>-1$
D. $x\neq - 1$
A. $x\geq - 1$且$x\neq0$
B. $x>1$
C. $x>-1$
D. $x\neq - 1$
答案:
C
5. [2024·潍坊期中]若$\sqrt{12}\cdot\sqrt{n}$的值是一个整数,则正整数$n$的最小值为 ( )
A. 1
B. 2
C. 3
D. 4
A. 1
B. 2
C. 3
D. 4
答案:
B
6. 若$\sqrt{a^{2}b}=a\sqrt{b}$成立,则$a,b$满足的条件是( )
A. $a<0$且$b>0$
B. $a\geq0$且$b\geq0$
C. $a<0$且$b\geq0$
D. $a\leq0$且$b\geq0$
A. $a<0$且$b>0$
B. $a\geq0$且$b\geq0$
C. $a<0$且$b\geq0$
D. $a\leq0$且$b\geq0$
答案:
B
7. 新考法 数形结合法 实数$a,b$在数轴上对应的点的位置如图所示,化简$\sqrt{(a + 1)^{2}}+\sqrt{(b - 1)^{2}}-\sqrt{(a - b)^{2}}$的结果是 ( )
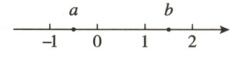
A. - 2
B. 2a
C. 2b
D. 0
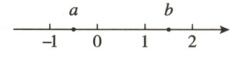
A. - 2
B. 2a
C. 2b
D. 0
答案:
B [点拨]由数轴得−1<a<0,1<b<2,
∴a + 1>0,b - 1>0,a - b<0。
∴$\sqrt{(a + 1)^{2}} + \sqrt{(b - 1)^{2}} - \sqrt{(a - b)^{2}}$ = |a + 1| + |b - 1| - |a - b| = a + 1 + b - 1 + a - b = 2a。
∴a + 1>0,b - 1>0,a - b<0。
∴$\sqrt{(a + 1)^{2}} + \sqrt{(b - 1)^{2}} - \sqrt{(a - b)^{2}}$ = |a + 1| + |b - 1| - |a - b| = a + 1 + b - 1 + a - b = 2a。
8. [2024·济南莱芜区期末]直角三角形两条直角边长分别为$\sqrt{5}-\sqrt{3}$和$\sqrt{5}+\sqrt{3}$,则该直角三角形斜边上的中线长为 ( )
A. $\frac{1}{2}$
B. $\sqrt{2}$
C. 1
D. 2
A. $\frac{1}{2}$
B. $\sqrt{2}$
C. 1
D. 2
答案:
D
9. 新视角 开放性试题 写出一个最简二次根式,使它与$\sqrt{12}$可以进行合并,这个二次根式可以是________.(写一个即可)
答案:
$\sqrt{3}$(答案不唯一)
10. [2024·烟台]若代数式$\frac{3}{\sqrt{x - 1}}$在实数范围内有意义,则$x$的取值范围为________.
答案:
x>1
11. [2024·营口期末]若$\sqrt{45}$与最简二次根式$\sqrt{m + 1}$是同类二次根式,则$m$的值为______.
答案:
4
12. [2024·德州月考]已知$m,n$为实数,且$m=\sqrt{n - 9}+\sqrt{9 - n}+4$,则$m - n=$________.
答案:
−5
13.(8分)计算:
(1)$\sqrt{18}-5\sqrt{2}$;
(2)$2\sqrt{12}\times\frac{\sqrt{3}}{4}\div\sqrt{2}$;
(3)$(\sqrt{\frac{4}{16}-\pi})^{0}+\sqrt[3]{8}+|\sqrt{3}-2|+(\frac{1}{2})^{-1}$;
(4)$(\sqrt{12}-\sqrt{27})\div\sqrt{3}-(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})$.
(1)$\sqrt{18}-5\sqrt{2}$;
(2)$2\sqrt{12}\times\frac{\sqrt{3}}{4}\div\sqrt{2}$;
(3)$(\sqrt{\frac{4}{16}-\pi})^{0}+\sqrt[3]{8}+|\sqrt{3}-2|+(\frac{1}{2})^{-1}$;
(4)$(\sqrt{12}-\sqrt{27})\div\sqrt{3}-(\sqrt{5}-\sqrt{3})(\sqrt{5}+\sqrt{3})$.
答案:
[解]
(1)$\sqrt{18} - 5\sqrt{2} = 3\sqrt{2} - 5\sqrt{2} = -2\sqrt{2}$
(2)$2\sqrt{12}×\frac{\sqrt{3}}{4} + \sqrt{2} = 4\sqrt{3}×\frac{\sqrt{3}}{4} + \sqrt{2} = 3 + \sqrt{2}$
(3)$(\sqrt{\frac{4}{16}} - \pi)^{0} + \sqrt{8} + |\sqrt{3} - 2| + (\frac{1}{2})^{-1} = 1 + 2\sqrt{2} + (2 - \sqrt{3}) + 2 = 1 + 2\sqrt{2} + 2 - \sqrt{3} + 2 = 5 + 2\sqrt{2} - \sqrt{3}$
(4)$(\sqrt{12} - \sqrt{27})÷\sqrt{3} - (\sqrt{5} - \sqrt{3})(\sqrt{5} + \sqrt{3}) = (2\sqrt{3} - 3\sqrt{3})÷\sqrt{3} - (5 - 3) = -1 - 2 = -3$
(1)$\sqrt{18} - 5\sqrt{2} = 3\sqrt{2} - 5\sqrt{2} = -2\sqrt{2}$
(2)$2\sqrt{12}×\frac{\sqrt{3}}{4} + \sqrt{2} = 4\sqrt{3}×\frac{\sqrt{3}}{4} + \sqrt{2} = 3 + \sqrt{2}$
(3)$(\sqrt{\frac{4}{16}} - \pi)^{0} + \sqrt{8} + |\sqrt{3} - 2| + (\frac{1}{2})^{-1} = 1 + 2\sqrt{2} + (2 - \sqrt{3}) + 2 = 1 + 2\sqrt{2} + 2 - \sqrt{3} + 2 = 5 + 2\sqrt{2} - \sqrt{3}$
(4)$(\sqrt{12} - \sqrt{27})÷\sqrt{3} - (\sqrt{5} - \sqrt{3})(\sqrt{5} + \sqrt{3}) = (2\sqrt{3} - 3\sqrt{3})÷\sqrt{3} - (5 - 3) = -1 - 2 = -3$
查看更多完整答案,请扫码查看


