2025年综合应用创新题典中点九年级数学下册鲁教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年综合应用创新题典中点九年级数学下册鲁教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
1. 下列各式中,属于二次根式的是 ( )
A. $\frac{1}{x}$
B. $2x + 1$
C. $\sqrt{5}$
D. $\sqrt[3]{6}$
A. $\frac{1}{x}$
B. $2x + 1$
C. $\sqrt{5}$
D. $\sqrt[3]{6}$
答案:
C
2. [2024·烟台福山区期中] 下列二次根式中:$\sqrt{10x}$,$\sqrt{x^{2}-2x + 1}$,$\sqrt{a^{2}-b^{2}}$,$\sqrt{\frac{x - y}{x}}$,$\sqrt{144x}$,属于最简二次根式的个数为 ( )
A. 1
B. 2
C. 3
D. 4
A. 1
B. 2
C. 3
D. 4
答案:
B
3. 与$-\sqrt{5}$是同类二次根式的是 ( )
A. $\sqrt{10}$
B. $\sqrt{15}$
C. $\sqrt{20}$
D. $\sqrt{25}$
A. $\sqrt{10}$
B. $\sqrt{15}$
C. $\sqrt{20}$
D. $\sqrt{25}$
答案:
C
4. [2024·潍坊一模] 使$\frac{\sqrt{3x + 7}}{x + 2}$有意义的$x$的取值范围是 ( )
A. $x\geqslant-\frac{7}{3}$且$x\neq - 2$
B. $x\geqslant-\frac{7}{3}$
C. $x\leqslant-\frac{7}{3}$
D. $x\geqslant - 2$
A. $x\geqslant-\frac{7}{3}$且$x\neq - 2$
B. $x\geqslant-\frac{7}{3}$
C. $x\leqslant-\frac{7}{3}$
D. $x\geqslant - 2$
答案:
A
5. 下面计算正确的是 ( )
A. $-(\sqrt{7})^{2}=-7$
B. $\sqrt{(-5)^{2}}=-5$
C. $\sqrt{24}=4\sqrt{6}$
D. $-(-\sqrt{\frac{9}{16}})=\frac{9}{16}$
A. $-(\sqrt{7})^{2}=-7$
B. $\sqrt{(-5)^{2}}=-5$
C. $\sqrt{24}=4\sqrt{6}$
D. $-(-\sqrt{\frac{9}{16}})=\frac{9}{16}$
答案:
A
6. 化简$|5 - x|+(\sqrt{3 - x})^{2}$的结果为________.
答案:
8 - 2x
7. $x^{2}-3$在有理数范围内不能进行因式分解,但$3 = (\sqrt{3})^{2}$,故$x^{2}-3 = x^{2}-(\sqrt{3})^{2}=(x - \sqrt{3})\cdot(x + \sqrt{3})$,这就把$x^{2}-3$在实数范围内进行了因式分解. 按照这个思路,$2a^{2}-14$在实数范围内因式分解的结果是__________.
答案:
2(a - $\sqrt{7}$)(a + $\sqrt{7}$)
8. 已知三角形的三边长分别为3,5,$k$,则化简$|9 - k|+\sqrt{(1 - k)^{2}}=$ ( )
A. 8
B. - 8
C. $2k - 10$
D. $10 - 2k$
A. 8
B. - 8
C. $2k - 10$
D. $10 - 2k$
答案:
A
9. [2024·枣庄月考] 实数$a$在数轴上对应的点的位置如图所示,则$\sqrt{(a - 4)^{2}}-\sqrt{(a - 11)^{2}}$化简后为 ( )
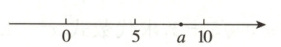
A. 7
B. - 7
C. $15 - 2a$
D. $2a - 15$
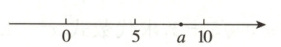
A. 7
B. - 7
C. $15 - 2a$
D. $2a - 15$
答案:
D【点拨】由数轴可知5 < a < 10,
∴a - 4 > 0,a - 11 < 0.
∴$\sqrt{(a - 4)^2}-\sqrt{(a - 11)^2}=a - 4-(11 - a)=a - 4 - 11 + a = 2a - 15$.
∴a - 4 > 0,a - 11 < 0.
∴$\sqrt{(a - 4)^2}-\sqrt{(a - 11)^2}=a - 4-(11 - a)=a - 4 - 11 + a = 2a - 15$.
10. 甲、乙两名同学做一道相同的题目.
化简求值:$\frac{1}{a}+\sqrt{\frac{1}{a^{2}}+a^{2}-2}$,其中$a = \frac{1}{5}$.
甲同学的解法:原式$=\frac{1}{a}+\sqrt{(\frac{1}{a}-a)^{2}}=\frac{1}{a}+|\frac{1}{a}-a|=\frac{1}{a}+\frac{1}{a}-a=\frac{2}{a}-a = 10-\frac{1}{5}=\frac{49}{5}$.
乙同学的解法:原式$=\frac{1}{a}+\sqrt{(a-\frac{1}{a})^{2}}=\frac{1}{a}+|a-\frac{1}{a}|=\frac{1}{a}+a-\frac{1}{a}=a=\frac{1}{5}$.
请问哪名同学的解法正确?请说明理由.
化简求值:$\frac{1}{a}+\sqrt{\frac{1}{a^{2}}+a^{2}-2}$,其中$a = \frac{1}{5}$.
甲同学的解法:原式$=\frac{1}{a}+\sqrt{(\frac{1}{a}-a)^{2}}=\frac{1}{a}+|\frac{1}{a}-a|=\frac{1}{a}+\frac{1}{a}-a=\frac{2}{a}-a = 10-\frac{1}{5}=\frac{49}{5}$.
乙同学的解法:原式$=\frac{1}{a}+\sqrt{(a-\frac{1}{a})^{2}}=\frac{1}{a}+|a-\frac{1}{a}|=\frac{1}{a}+a-\frac{1}{a}=a=\frac{1}{5}$.
请问哪名同学的解法正确?请说明理由.
答案:
【解】甲同学的解法正确.理由如下:
$\sqrt{\frac{1}{a^2}+a^2 - 2}=\sqrt{(\frac{1}{a}-a)^2}=|\frac{1}{a}-a|$.
∵a = $\frac{1}{5}$,
∴$\frac{1}{a}=5$,
∴$\frac{1}{a}>a$.
∴$\frac{1}{a}-a>0$.
∴$|\frac{1}{a}-a|=\frac{1}{a}-a$.乙同学在去绝对值符号时忽略了$\frac{1}{a}$与 a 的大小关系,导致错误.
$\sqrt{\frac{1}{a^2}+a^2 - 2}=\sqrt{(\frac{1}{a}-a)^2}=|\frac{1}{a}-a|$.
∵a = $\frac{1}{5}$,
∴$\frac{1}{a}=5$,
∴$\frac{1}{a}>a$.
∴$\frac{1}{a}-a>0$.
∴$|\frac{1}{a}-a|=\frac{1}{a}-a$.乙同学在去绝对值符号时忽略了$\frac{1}{a}$与 a 的大小关系,导致错误.
查看更多完整答案,请扫码查看


