第99页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
10. [教材 P136 习题 T8 变式题][2025·岳阳期中]如图,在等边三角形 ABC 中,BD 平分∠ABC,E 是 BC 延长线上一点,且 CE = CD,连接 DE,则∠BDE 的度数为
]
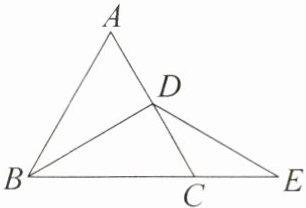
120°
。]

答案:
120°
11. 如图,将边长为 5 cm 的等边三角形 ABC 向右平移 1 cm 得到△A'B'C',此时阴影部分的周长为
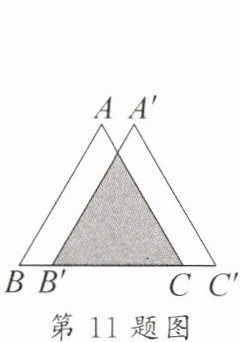
12 cm
。
答案:
12 cm
12. 新考向情境题 如图,上午 8 时,一条渔船从港口 A 出发,以 15 n mile/h 的速度向正北方向 AN 航行,上午 10 时到达海岛 B 处,从 A,B 处观测海岛 C,测得∠NAC = 30°,∠NBC = 60°.
(1)从海岛 B 到海岛 C 的距离为
(2)渔船从海岛 B 按原来的方向继续航行 30 n mile 到达海岛 D 处,则从海岛 C 到海岛 D 的距离为
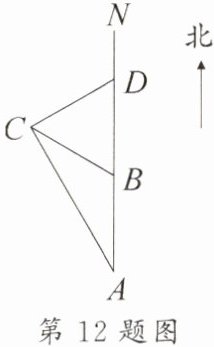
(1)从海岛 B 到海岛 C 的距离为
30
n mile;(2)渔船从海岛 B 按原来的方向继续航行 30 n mile 到达海岛 D 处,则从海岛 C 到海岛 D 的距离为
30
n mile.
答案:
(1)30
(2)30
(1)30
(2)30
13. [2025·邵阳大祥区期末]如图,△ABC 是等边三角形,D 为边 BC 的中点,BE⊥AB 交 AD 的延长线于点 E,点 F 在 AE 上,且 AF = BE,连接 CF,CE. 求证:
(1)∠CAF = ∠CBE;
(2)△CEF 是等边三角形.
]
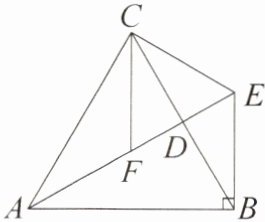
(1)∠CAF = ∠CBE;
(2)△CEF 是等边三角形.
]

答案:
(1)
∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠ABC=60°。
∵D为BC中点,AD平分∠BAC(等边三角形三线合一),
∴∠CAF=∠BAC/2=30°。
∵BE⊥AB,
∴∠ABE=90°,
∴∠CBE=∠ABE-∠ABC=90°-60°=30°。
∴∠CAF=∠CBE。
(2) 在△AFC和△BEC中,
∵AC=BC,∠CAF=∠CBE(已证),AF=BE(已知),
∴△AFC≌△BEC(SAS)。
∴CF=CE,∠ACF=∠BCE。
∵∠ACB=∠ACF+∠FCB=60°,
∴∠BCE+∠FCB=∠FCE=60°。
∵CF=CE且∠FCE=60°,
∴△CEF是等边三角形。
(1)
∵△ABC是等边三角形,
∴AC=BC,∠BAC=∠ABC=60°。
∵D为BC中点,AD平分∠BAC(等边三角形三线合一),
∴∠CAF=∠BAC/2=30°。
∵BE⊥AB,
∴∠ABE=90°,
∴∠CBE=∠ABE-∠ABC=90°-60°=30°。
∴∠CAF=∠CBE。
(2) 在△AFC和△BEC中,
∵AC=BC,∠CAF=∠CBE(已证),AF=BE(已知),
∴△AFC≌△BEC(SAS)。
∴CF=CE,∠ACF=∠BCE。
∵∠ACB=∠ACF+∠FCB=60°,
∴∠BCE+∠FCB=∠FCE=60°。
∵CF=CE且∠FCE=60°,
∴△CEF是等边三角形。
14. 新考向类比探究 如图①,△ABC 为等边三角形,AM⊥BC 于点 M,D 是 BC 边上异于点 B,C 的任意一点,DE⊥AB 于点 E,DF⊥AC 于点 F.
(1)若 AM = 10,则 DE + DF =
(2)【问题探究】探究 AM,DE,DF 的数量关系并证明.
(3)【拓展应用】如图②,在等边三角形 ABC 中,P 是 AB 上一点,过点 P 作 PD⊥BC,PE⊥AC,垂足分别为点 D,E,连接 PC. 若△ABC 的面积是 4√3,BC = 4,则 PC + PD + PE 的最小值是
(1)若 AM = 10,则 DE + DF =
10
。(2)【问题探究】探究 AM,DE,DF 的数量关系并证明.
$AM=DE+DF$.证明略.
(3)【拓展应用】如图②,在等边三角形 ABC 中,P 是 AB 上一点,过点 P 作 PD⊥BC,PE⊥AC,垂足分别为点 D,E,连接 PC. 若△ABC 的面积是 4√3,BC = 4,则 PC + PD + PE 的最小值是
$4\sqrt{3}$
。
答案:
(1)10
(2)$AM=DE+DF$.证明略.
(3)$4\sqrt{3}$
(1)10
(2)$AM=DE+DF$.证明略.
(3)$4\sqrt{3}$
查看更多完整答案,请扫码查看


