《2025年状元成才路创优作业八年级数学上册湘教版》

8. 下列说法正确的是(C)

A.真命题的逆命题一定是真命题
B.假命题的逆命题一定是假命题
C.所有的定理一定有逆命题
D.所有的定理一定有逆定理

答案： C

9. 已知△ABC,用“锐角”“直角”或“钝角”填空：
(1)若∠A : ∠B : ∠C = 1 : 3 : 5,则△ABC 是钝角三角形；
(2)若分别与∠A,∠B,∠C 相邻的外角的度数之比为 3 : 4 : 5,则△ABC 是直角三角形.

答案：
(1)钝角　
(2)直角

10. 如图,AB // CD,DE 与 BF 相交于点 E,求证：∠3 = ∠1 + ∠2 - 180°.

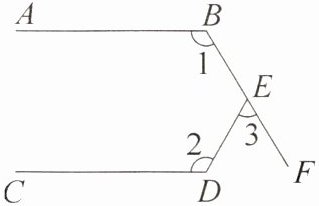
答案： 过点 $E$ 作 $EG // AB$。
由于 $AB // CD$，根据平行线的传递性：
如果两条直线都与第三条直线平行，那么这两条直线也平行，
可得 $EG // CD$。
根据平行线的性质：
两直线平行，同旁内角互补，
因为$EG // CD$，
则 $\angle GED + \angle 2 = 180°$，
所以$\angle GED = 180° - \angle 2$。
根据平行线的性质：
两直线平行，内错角相等，
因为$EG // AB$，
则 $\angle BEG = \angle 1$。
因为$\angle 3 = \angle BEG - \angle GED$，
代入$\angle BEG = \angle 1$，$\angle GED = 180° - \angle 2$，
可得：
$\angle 3 = \angle 1 - (180° - \angle 2)$
$\angle 3 = \angle 1 + \angle 2 - 180°$
综上，证明了 $\angle 3 = \angle 1 + \angle 2 - 180°$。

11. 新考向 项目式学习·证明三角形的内角和定理


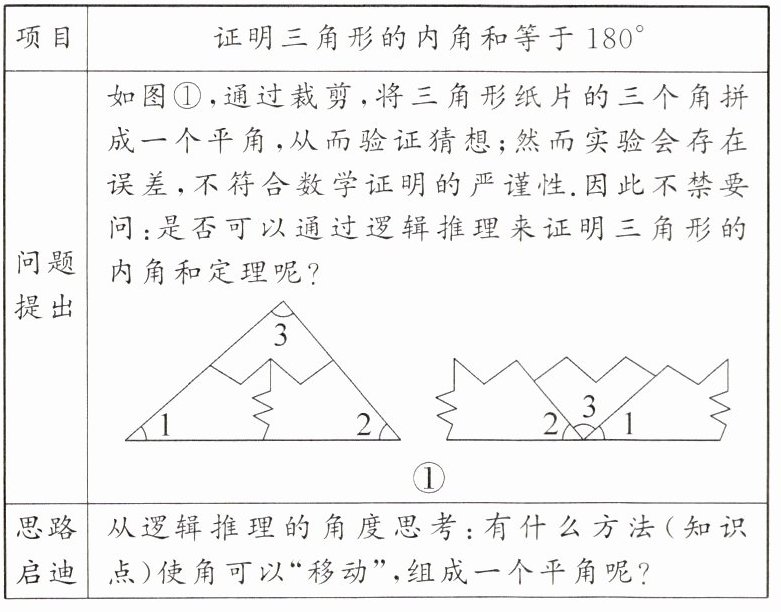
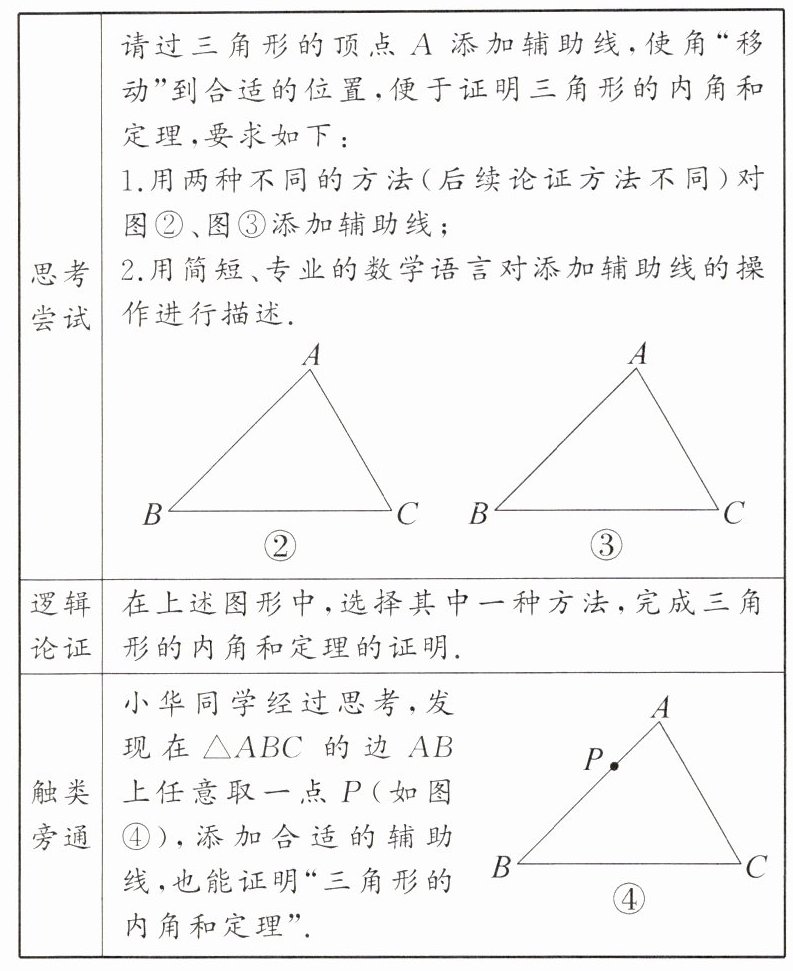
(1)完成“思考尝试”中的操作与描述；
(2)写出“逻辑论证”中的证明过程；
(3)写出“触类旁通”中的证明过程.

答案：

(1)解:如图②,过点A作MN//BC.

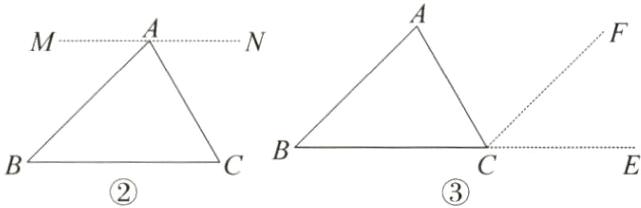
如图③,延长BC至点E，过点C作CF//AB.
(2)证明:如图②,因为MN//BC,
所以∠B=∠MAB,∠C=∠NAC.
因为∠MAB+∠BAC+∠NAC=180°,
所以∠B+∠BAC+∠C=180°.
(或如图③,因为CF//AB,
所以∠B=∠ECF,∠A=∠ACF.
因为∠ACB+∠ACF+∠ECF=180°,
所以∠ACB+∠A+∠B=180°.)
(3)证明:如图④，过点P作PM//BC交AC于M,作PQ//AC交BC于点Q.

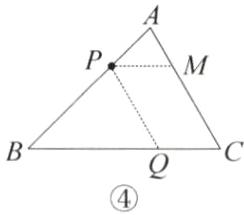
因为PM//BC,
所以∠APM=∠B,∠MPQ=∠BQP.
因为PQ//AC,
所以∠C=∠BQP、∠A=∠BPQ,
所以∠C=∠MPQ.
因为∠APM+∠MPQ+∠BPQ=180°,
所以∠B+∠C+∠A=180°.