《2025年状元成才路创优作业八年级数学上册湘教版》

【教材母题】“将军饮马”问题具体如下：有一位将军从A地出发到河边CD饮马,然后再回到B地,如图所示。如何确定饮马地点P,使得路程AP+BP最短？

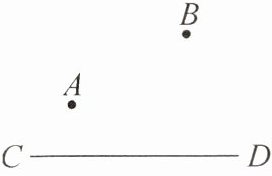
模型归纳：点A,B在直线l的同侧,在直线l上找一点P,使PA+PB的值最小。
作法：如图,作点B关于直线l的对称点B',连接AB',与直线l的交点即为所求点P。因为PA+PB= PA+PB'≥AB'(两点之间,线段最短),所以PA+PB的最小值为AB'的长。

答案： 作点 B 关于 CD 的对称点 B'，连接 AB'交 CD 于点 P，P 即为所求。

1. [2025·北海期末]如图,在△ABC中,直线m是线段BC的垂直平分线,点P是直线m上的一个动点。若AB= 7,AC= 4,BC= 5,则△APC周长的最小值是(B)

A.12
B.11
C.9
D.7

答案： B

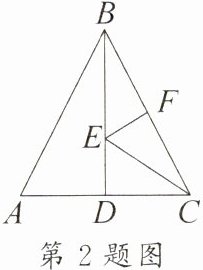
2. 如图,在△ABC中,AB= BC= 8,△ABC的面积是24,D为AC的中点,E为线段BD上的动点,F为边BC上的动点,则CE+EF的最小值为6。

答案： 6

变式题 [条件变式]如图,在等腰三角形ABC中,用尺规作出射线AD。若AB= AC= 5,AD= 4,BC= 6,M,N分别是线段AD和线段AB上的动点,则BM+MN的最小值为______。

答案： 4.8

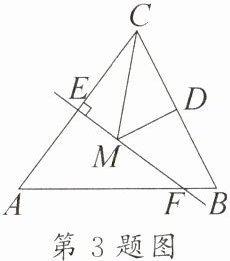
3. [2025·怀化通道县期中]如图,等腰三角形ABC的底边BC的长为6,面积是18,腰AC的垂直平分线EF分别交AC,AB于点E,F。若D为BC边的中点,M为线段EF上一动点,则△CDM的周长的最小值为9。

答案： 9

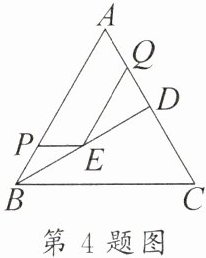
4. [2025·邵阳大祥区期末]如图,在等边三角形ABC中,BD是中线,点P,Q分别在AB,AD上,且BP= AQ= QD= 1,动点E在BD上,则PE+QE的最小值为3。

答案： 3

5. 在某草原上,有两条交叉且笔直的公路OA,OB,如图,∠AOB= 30°,在两条公路之间的点P处有一个草场,OP= 4。现在在两条公路上各有一户牧民在移动放牧,分别记为M,N,存在M,N使得△PMN的周长最小。请找出M,N的位置,并求出△PMN的周长的最小值。

答案：
解:如图,作点 P 关于直线 OA 的对称点 F,作点 P 关于直线 OB 的对称点 G,连接 FG,分别交 OA,OB 于点 M,N,连接 OG,OF.所以 MP=MF,NP=NG,易知△PMN 周长的最小值为 FG.
由轴对称的性质,得∠AOF=∠AOP,∠POB=∠GOB,OP=OF,OP=OG.
因为∠AOP+∠POB=∠AOB=30°,OP=4,
所以∠FOG=∠AOF+∠AOP+∠POB+∠GOB=60°,OF=OG=4,
所以△FOG 为边长为 4 的等边三角形,所以 FG=4,
所以△PMN 的周长的最小值为 4.