第111页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
[2025·常德临澧县期末改编]为了测量一条两岸平行的河流的宽度,三个数学活动小组设计了不同的方案,他们在河南岸的点$B处测得河北岸的树A恰好在B$的正北方向,测量方案如下表:
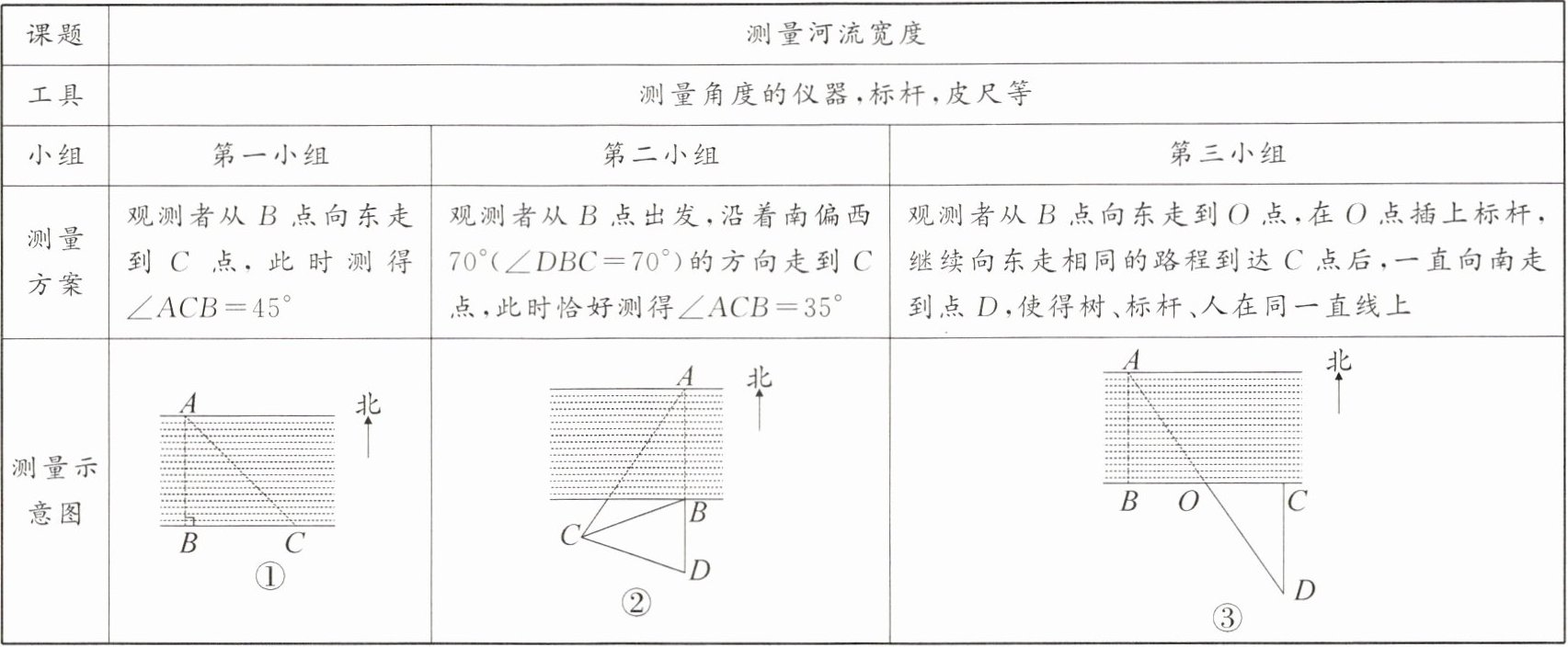
(1)由第一小组的方案可知,河宽$AB$的长度就是线段
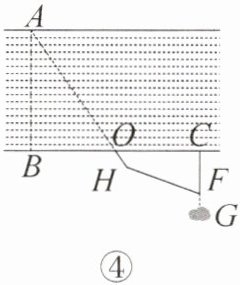
(2)第三小组在实际测量中,从点$C走到点F处时发现前方有大石头G$挡路(如图④),他们商议后决定改变路线,测得$∠BAO = 35^{\circ}$后,他们向右转$110^{\circ}(∠GFH = 110^{\circ})继续前行至点H$,使点$A$,$O$,$H$在一条直线上。他们认为只要测得$CF和FH的长就可求出河宽AB$的长,你认为他们的方案是否可行?如果可行,请给出证明;如果不可行,请说明理由。
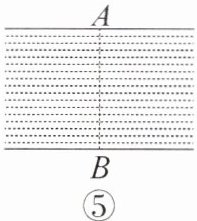
(3)请你设计一个测量方案,在图⑤中画出示意图,指明只要测出哪条线段的长,就能推算出河宽$AB$的长,并证明方案的可行性。

(1)由第一小组的方案可知,河宽$AB$的长度就是线段
BC
的长度;第二小组测得$BC = 30m$,则$AB = $30
$m$。(2)第三小组在实际测量中,从点$C走到点F处时发现前方有大石头G$挡路(如图④),他们商议后决定改变路线,测得$∠BAO = 35^{\circ}$后,他们向右转$110^{\circ}(∠GFH = 110^{\circ})继续前行至点H$,使点$A$,$O$,$H$在一条直线上。他们认为只要测得$CF和FH的长就可求出河宽AB$的长,你认为他们的方案是否可行?如果可行,请给出证明;如果不可行,请说明理由。

第三小组的方案可行.证明如下:
如图④,延长AH交CF的延长线于点E.
因为O是BC的中点,AB⊥BC,CE⊥BC,
所以OB=OC,∠ABO=∠ECO=90°.
在△ABO和△ECO中,{∠ABO=∠ECO,
OB=OC,
∠AOB=∠EOC,
所以△ABO≌△ECO(角边角).
所以AB=EC,∠E=∠BAO=35°.
所以在△EFH中,
∠FHE=180°−∠E−∠EFH=180°−35°−110°=35°.
所以∠FHE=∠E,所以EF=FH.
所以CE=CF+EF=CF+FH,所以AB=CF+FH.
故第三小组的方案可行.
如图④,延长AH交CF的延长线于点E.
因为O是BC的中点,AB⊥BC,CE⊥BC,
所以OB=OC,∠ABO=∠ECO=90°.
在△ABO和△ECO中,{∠ABO=∠ECO,
OB=OC,
∠AOB=∠EOC,
所以△ABO≌△ECO(角边角).
所以AB=EC,∠E=∠BAO=35°.
所以在△EFH中,
∠FHE=180°−∠E−∠EFH=180°−35°−110°=35°.
所以∠FHE=∠E,所以EF=FH.
所以CE=CF+EF=CF+FH,所以AB=CF+FH.
故第三小组的方案可行.
(3)请你设计一个测量方案,在图⑤中画出示意图,指明只要测出哪条线段的长,就能推算出河宽$AB$的长,并证明方案的可行性。

如图⑤,观测者从B点向正西走到C点,使用测量角度的仪器测得∠BCD=∠ACB,CD交AB的延长线于点D,只要测出DB的长,就能推算出河宽AB的长.
证明如下:
因为AB⊥BC,所以∠ABC=∠DBC=90°.
在△ABC和△DBC中,{∠ABC=∠DBC,
BC=BC,
∠ACB=∠DCB,
所以△ABC≌△DBC(角边角),所以AB=DB.
所以河宽AB的长等于线段DB的长.
证明如下:
因为AB⊥BC,所以∠ABC=∠DBC=90°.
在△ABC和△DBC中,{∠ABC=∠DBC,
BC=BC,
∠ACB=∠DCB,
所以△ABC≌△DBC(角边角),所以AB=DB.
所以河宽AB的长等于线段DB的长.
答案:
(1)BC 30
(2)第三小组的方案可行.证明如下:
如图④,延长AH交CF的延长线于点E.
因为O是BC的中点,AB⊥BC,CE⊥BC,
所以OB=OC,∠ABO=∠ECO=90°.
在△ABO和△ECO中,{∠ABO=∠ECO,
OB=OC,
∠AOB=∠EOC,
所以△ABO≌△ECO(角边角).
所以AB=EC,∠E=∠BAO=35°.
所以在△EFH中,
∠FHE=180°−∠E−∠EFH=180°−35°−110°=35°.
所以∠FHE=∠E,所以EF=FH.
所以CE=CF+EF=CF+FH,所以AB=CF+FH.
故第三小组的方案可行.
(3)如图⑤,观测者从B点向正西走到C点,使用测量角度的仪器测得∠BCD=∠ACB,CD交AB的延长线于点D,只要测出DB的长,就能推算出河宽AB的长.
证明如下:
因为AB⊥BC,所以∠ABC=∠DBC=90°.
在△ABC和△DBC中,{∠ABC=∠DBC,
BC=BC,
∠ACB=∠DCB,
所以△ABC≌△DBC(角边角),所以AB=DB.
所以河宽AB的长等于线段DB的长.
(1)BC 30
(2)第三小组的方案可行.证明如下:
如图④,延长AH交CF的延长线于点E.
因为O是BC的中点,AB⊥BC,CE⊥BC,
所以OB=OC,∠ABO=∠ECO=90°.
在△ABO和△ECO中,{∠ABO=∠ECO,
OB=OC,
∠AOB=∠EOC,
所以△ABO≌△ECO(角边角).
所以AB=EC,∠E=∠BAO=35°.
所以在△EFH中,
∠FHE=180°−∠E−∠EFH=180°−35°−110°=35°.
所以∠FHE=∠E,所以EF=FH.
所以CE=CF+EF=CF+FH,所以AB=CF+FH.
故第三小组的方案可行.
(3)如图⑤,观测者从B点向正西走到C点,使用测量角度的仪器测得∠BCD=∠ACB,CD交AB的延长线于点D,只要测出DB的长,就能推算出河宽AB的长.
证明如下:
因为AB⊥BC,所以∠ABC=∠DBC=90°.
在△ABC和△DBC中,{∠ABC=∠DBC,
BC=BC,
∠ACB=∠DCB,
所以△ABC≌△DBC(角边角),所以AB=DB.
所以河宽AB的长等于线段DB的长.
查看更多完整答案,请扫码查看


