第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 已知两角及其夹边作三角形,所用的基本作图方法是(
A.平分已知角
B.作已知直线的垂线
C.作一个角等于已知角及作一条线段等于已知线段
D.作已知直线的平行线
C
)A.平分已知角
B.作已知直线的垂线
C.作一个角等于已知角及作一条线段等于已知线段
D.作已知直线的平行线
答案:
C
2. [教材P127练习T1变式题]如图,已知线段a,b,∠α,∠β.求作△ABC,使BC = a + b,∠B = ∠α,∠C = ∠β(保留作图痕迹,不要求写出作法).
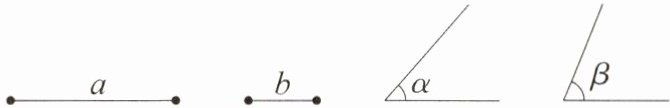
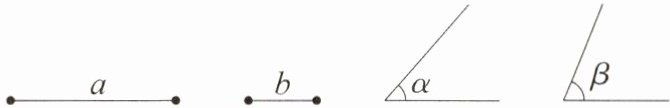
答案:
1. 作射线BM,在射线BM上截取BD=a,再以D为端点在射线DM上截取DC=b,得BC=a+b;
2. 以点B为顶点,BC为一边,作∠CBE=∠α;
3. 以点C为顶点,CB为一边,在BC同侧作∠BCF=∠β,射线BE与CF交于点A;
4. △ABC即为所求(保留作图痕迹)。
2. 以点B为顶点,BC为一边,作∠CBE=∠α;
3. 以点C为顶点,CB为一边,在BC同侧作∠BCF=∠β,射线BE与CF交于点A;
4. △ABC即为所求(保留作图痕迹)。
3. (1)如图,已知∠ACB,过点A作射线AD,使AD//BC,且点B,D在边CA的异侧(保留作图痕迹,不要求写出作法);
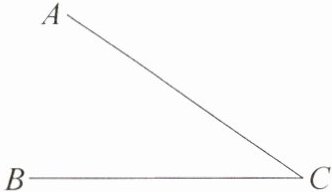
(2)上述作图依据是

(2)上述作图依据是
内错角相等,两直线平行
.
答案:
1. (1)作图:
以点$A$为顶点,在$CA$的另一侧作$\angle CAD=\angle ACB$,射线$AD$即为所求(作图痕迹:用圆规以$C$为圆心,任意长为半径画弧,交$CB$、$CA$于两点$M$、$N$;再以$A$为圆心,$CM$长为半径画弧,交$CA$于点$P$;然后以$P$为圆心,$MN$长为半径画弧,与前弧交于点$Q$,连接$AQ$并延长得到射线$AD$)。
2. (2)答案:
内错角相等,两直线平行(因为$\angle CAD=\angle ACB$,$\angle CAD$与$\angle ACB$是内错角,根据平行线的判定定理:$\boldsymbol{\angle 1=\angle 2\Rightarrow l_1// l_2}$($\angle 1$,$\angle 2$是内错角,$l_1$,$l_2$是两条直线))。
故答案为:内错角相等,两直线平行。
以点$A$为顶点,在$CA$的另一侧作$\angle CAD=\angle ACB$,射线$AD$即为所求(作图痕迹:用圆规以$C$为圆心,任意长为半径画弧,交$CB$、$CA$于两点$M$、$N$;再以$A$为圆心,$CM$长为半径画弧,交$CA$于点$P$;然后以$P$为圆心,$MN$长为半径画弧,与前弧交于点$Q$,连接$AQ$并延长得到射线$AD$)。
2. (2)答案:
内错角相等,两直线平行(因为$\angle CAD=\angle ACB$,$\angle CAD$与$\angle ACB$是内错角,根据平行线的判定定理:$\boldsymbol{\angle 1=\angle 2\Rightarrow l_1// l_2}$($\angle 1$,$\angle 2$是内错角,$l_1$,$l_2$是两条直线))。
故答案为:内错角相等,两直线平行。
4. [2025·邵阳新宁县期末]如图,在△ABC中,AB>AC,∠CAD为△ABC的外角,观察图中尺规作图的痕迹,则下列结论错误的是(
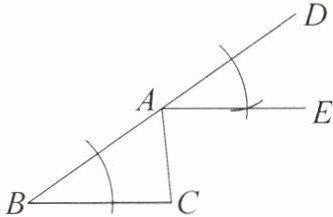
A.∠DAE = ∠B
B.∠EAC = ∠C
C.AE//BC
D.∠DAE = ∠EAC
D
)
A.∠DAE = ∠B
B.∠EAC = ∠C
C.AE//BC
D.∠DAE = ∠EAC
答案:
D
5. 学校将要举行篮球比赛,为了给运动员加油,某班提前给每位同学制作了一面相同规格的三角形彩旗,小明回家后发现自己的彩旗损坏了一角(如图),他想用彩纸重新制作一面完全相同的彩旗.请你帮助小明完成作图,并说明作图理由.
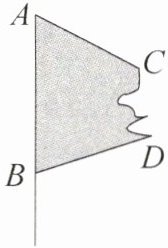

答案:
作图步骤:
1. 作线段 $ A'B' = AB $;
2. 以 $ A' $ 为顶点,$ A'B' $ 为一边,在 $ A'B' $ 同侧作 $ \angle DA'B' = \angle DAB $;
3. 以 $ B' $ 为顶点,$ A'B' $ 为一边,在 $ A'B' $ 同侧作 $ \angle EB'A' = \angle EBA $,射线 $ A'D $ 与 $ B'E $ 交于点 $ C' $;
4. $ \triangle A'B'C' $ 即为所求作的三角形。
作图理由:
在 $ \triangle ABC $ 和 $ \triangle A'B'C' $ 中,
$ \angle A = \angle A' $,$ AB = A'B' $,$ \angle B = \angle B' $,
根据“两角及其夹边对应相等的两个三角形全等”(ASA),
可得 $ \triangle ABC \cong \triangle A'B'C' $,故 $ \triangle A'B'C' $ 与原彩旗完全相同。
1. 作线段 $ A'B' = AB $;
2. 以 $ A' $ 为顶点,$ A'B' $ 为一边,在 $ A'B' $ 同侧作 $ \angle DA'B' = \angle DAB $;
3. 以 $ B' $ 为顶点,$ A'B' $ 为一边,在 $ A'B' $ 同侧作 $ \angle EB'A' = \angle EBA $,射线 $ A'D $ 与 $ B'E $ 交于点 $ C' $;
4. $ \triangle A'B'C' $ 即为所求作的三角形。
作图理由:
在 $ \triangle ABC $ 和 $ \triangle A'B'C' $ 中,
$ \angle A = \angle A' $,$ AB = A'B' $,$ \angle B = \angle B' $,
根据“两角及其夹边对应相等的两个三角形全等”(ASA),
可得 $ \triangle ABC \cong \triangle A'B'C' $,故 $ \triangle A'B'C' $ 与原彩旗完全相同。
6. [T2变式]如图,已知∠α,∠β,线段a,求作△ABC,使∠A = ∠α,∠B = ∠β,BC = a.
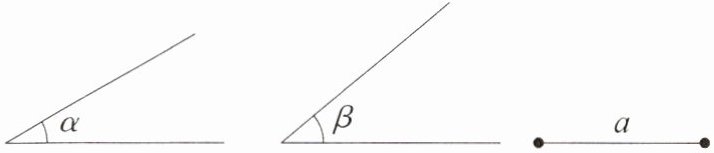

答案:
1. 作线段BC=a。
2. 以点B为顶点,BC为一边,作∠CBE=∠β(作角步骤:以∠β顶点为圆心,任意长为半径画弧交两边于M、N;以B为圆心,同长为半径画弧交BC于P;以P为圆心,MN长为半径画弧交前弧于Q,连BQ并延长得射线BE)。
3. 计算∠C=180°-∠α-∠β,以点C为顶点,BC为一边,作∠BCF=∠C(作角步骤:作平角∠COD=180°;作∠JOD=∠α,∠JON=∠β,则∠CON=∠C;同步骤2作∠BCF=∠CON得射线CF)。
4. 射线BE与CF交于点A,△ABC即为所求。
2. 以点B为顶点,BC为一边,作∠CBE=∠β(作角步骤:以∠β顶点为圆心,任意长为半径画弧交两边于M、N;以B为圆心,同长为半径画弧交BC于P;以P为圆心,MN长为半径画弧交前弧于Q,连BQ并延长得射线BE)。
3. 计算∠C=180°-∠α-∠β,以点C为顶点,BC为一边,作∠BCF=∠C(作角步骤:作平角∠COD=180°;作∠JOD=∠α,∠JON=∠β,则∠CON=∠C;同步骤2作∠BCF=∠CON得射线CF)。
4. 射线BE与CF交于点A,△ABC即为所求。
查看更多完整答案,请扫码查看


