第86页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
1. 如图,为了测量点 $ B $ 与河对面的目标 $ A $ 之间的距离,在点 $ B $ 同侧选择了一点 $ C $,测得 $ \angle ABC = 65^{\circ} $,$ \angle ACB = 35^{\circ} $,然后在 $ M $ 处立了标杆,使 $ \angle MBC = 65^{\circ} $,$ \angle MCB = 35^{\circ} $,得到 $ \triangle MBC \cong \triangle ABC $,所以测得 $ MB $ 的长就是 $ A $,$ B $ 间的距离,这里直接判定 $ \triangle MBC \cong \triangle ABC $ 的依据是(

A.边角边
B.角角边
C.边边边
D.角边角
D
)
A.边角边
B.角角边
C.边边边
D.角边角
答案:
D
2. 如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块。小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为 $ \triangle ABC $,提供下列各组元素的数据,配出来的玻璃不一定符合要求的是(
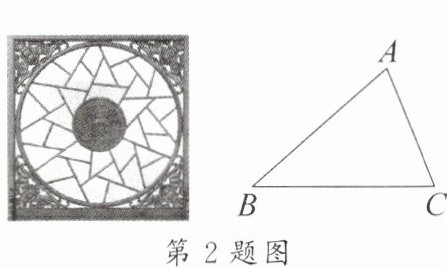
A.$ AB $,$ BC $,$ AC $
B.$ AB $,$ BC $,$ \angle B $
C.$ AB $,$ AC $,$ \angle B $
D.$ \angle A $,$ \angle B $,$ BC $
C
)
A.$ AB $,$ BC $,$ AC $
B.$ AB $,$ BC $,$ \angle B $
C.$ AB $,$ AC $,$ \angle B $
D.$ \angle A $,$ \angle B $,$ BC $
答案:
C
3. 新考向 情境题·电脑桌 如图①是一个可调节高度的电脑桌,它的工作原理是利用液体在封闭的管路中传递力和能量。如图②是其正面示意图,等长的支架 $ AD $,$ BC $ 交于它们的中点 $ E $,液压杆 $ FG // BC $。若 $ \angle ABE = 53^{\circ} $,则 $ \angle FGD $ 的度数为

53°
。
答案:
53°
4. 如图,为了测量一个池塘的长度 $ CF $,童童在池塘的两边各取点 $ B $,$ E $,使得点 $ B $,$ F $,$ C $,$ E $ 在同一条直线 $ l $ 上,然后在直线 $ l $ 的两侧分别取点 $ A $,$ D $,使得 $ AB // DE $,测得 $ \angle A = \angle D $,$ AC = DF $。若 $ BE = 20\ m $,$ BF = 5\ m $,则池塘的长度 $ CF $ 为

10
$m$。
答案:
10
5. 小明想知道一堵墙上的点 $ A $ 到地面的高度 $ OA $,$ OA \perp OD $,于是设计了如下方案:①找一根长度大于 $ OA $ 的直杆,使直杆靠在墙上,且顶端与点 $ A $ 重合,记下直杆与地面的夹角 $ \angle ABO $;②使直杆顶端竖直缓慢下滑,直到直杆与墙的夹角 $ \angle DCO = \angle ABO $,标记此时直杆的底端点 $ D $;③测量 $ OD $ 的长度,即为点 $ A $ 到地面的高度 $ OA $。请说明小明这样测量的理由。


答案:
在Rt△ABO和Rt△DCO中,
∠AOB=∠DOC=90°(OA⊥OD,OC⊥OD),
∠ABO=∠DCO(已知),
AB=CD(同一根直杆,长度不变),
∴Rt△ABO≌Rt△DCO(AAS),
∴OA=OD(全等三角形对应边相等)。
故测量OD的长度即为点A到地面的高度OA。
∠AOB=∠DOC=90°(OA⊥OD,OC⊥OD),
∠ABO=∠DCO(已知),
AB=CD(同一根直杆,长度不变),
∴Rt△ABO≌Rt△DCO(AAS),
∴OA=OD(全等三角形对应边相等)。
故测量OD的长度即为点A到地面的高度OA。
6. [2025·永州冷水滩区期末]状状为了测量楼高 $ AB $,在旗杆 $ CD $ 与楼之间选定一点 $ P $,测得视线 $ PC $ 与地面夹角 $ \angle DPC = 36^{\circ} $,视线 $ PA $ 与地面夹角 $ \angle APB = 54^{\circ} $,点 $ P $ 到楼底距离 $ PB $ 与旗杆高度均为 $ 10\ m $,旗杆与楼之间的距离 $ DB = 36\ m $,状状据此计算出了楼高 $ AB $ 是

26
$m$。
答案:
26
查看更多完整答案,请扫码查看


