《2025年全效学习同步学练测八年级数学上册湘教版》

8. 计算：
(1)$\dfrac{\sqrt{27}}{\sqrt{3}}$；
(2)$\sqrt{72}÷ \sqrt{6}$；
(3)$\dfrac{3\sqrt{24}}{6\sqrt{2}}$；
(4)$\dfrac{\sqrt{6a^{2}b}}{\sqrt{3ab}}(a＞0,b＞0)$；
(5)$4\sqrt{7}÷ \dfrac{2}{3}\sqrt{2}$。

答案： $8. (1)3 (2)2\sqrt{3} (3)\sqrt{3} (4)\sqrt{2a} (5)3\sqrt{14}$

$9. $计算$\sqrt{20}× \dfrac{\sqrt{3}}{4}÷ \sqrt{15}$的结果是　　$\frac{1}{2}$　　。　　

答案： $9. \frac{1}{2}$

$10. $站在海拔高度为$h\ m$的地方看到可见的水平距离为$d\ m，$它们近似地符合公式$d = 8\sqrt{\dfrac{h}{5}}。$如果某一登山者从海拔$n\ m$处登上海拔$2n\ m$高的山顶，那么他看到的水平距离是原来的　　$\sqrt{2}$　　倍。　　

答案： $10. \sqrt{2}$

11. 先化简，再求值：$\dfrac{a - 1}{a^{2}-2a + 1}÷ \left(\dfrac{a^{2}+a}{a^{2}-1}+\dfrac{1}{a - 1}\right)$，其中$a=\sqrt{3}-1$。

答案： $11. \frac{1}{a+1} $原式$=\frac{\sqrt{3}}{3}$

12. 如图，长方形纸板的面积为$30\sqrt{6}\ cm^{2}$，一边长为$3\sqrt{10}\ cm$，折叠纸板一次得到一个正方形，求该正方形的面积。

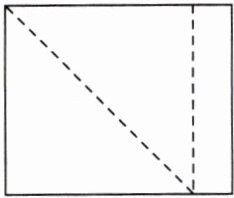
答案： 12. 该正方形的面积为$ 60 cm^2$

13. 【运算能力】老师在讲授“二次根式”时，在黑板上写出下面的一道题作为练习：
已知$\sqrt{7}=a$，$\sqrt{70}=b$，用含$a$，$b$的代数式表示$\sqrt{4.9}$。
小豪、小麦两名同学跑上讲台，写了下面两种解法：
小豪：$\sqrt{4.9}=\sqrt{\dfrac{49}{10}}=\sqrt{\dfrac{49× 10}{10× 10}}=\sqrt{\dfrac{490}{100}}=\dfrac{\sqrt{7× 70}}{10}=\dfrac{\sqrt{7}× \sqrt{70}}{10}=\dfrac{ab}{10}$。
小麦：$\sqrt{4.9}=\sqrt{49× 0.1}=7\sqrt{0.1}$。
因为$\sqrt{0.1}=\sqrt{\dfrac{1}{10}}=\sqrt{\dfrac{7}{70}}=\dfrac{\sqrt{7}}{\sqrt{70}}=\dfrac{a}{b}$，
所以$\sqrt{4.9}=7\sqrt{0.1}=\dfrac{7a}{b}$。
老师看后，提出下面的问题：
(1)两名同学的解法都正确吗？
(2)请你再给出一种不同于两人的解法。

答案： $(1)$判断两名同学解法是否正确
小豪的解法：
根据二次根式的性质$\sqrt{\frac{m}{n}}=\frac{\sqrt{m}}{\sqrt{n}}$（$m\geq0,n ＞ 0$）以及$\sqrt{mn}=\sqrt{m}\cdot\sqrt{n}$（$m\geq0,n\geq0$），对$\sqrt{4.9}=\sqrt{\frac{49}{10}}$进行逐步化简，最后得到$\frac{\sqrt{7}×\sqrt{70}}{10}$，再代入$\sqrt{7}=a$，$\sqrt{70}=b$，得到$\frac{ab}{10}$，过程正确。
小麦的解法：
先将$\sqrt{4.9}$变形为$7\sqrt{0.1}$，然后根据二次根式的性质$\sqrt{\frac{m}{n}}=\frac{\sqrt{m}}{\sqrt{n}}$（$m\geq0,n ＞ 0$），把$\sqrt{0.1}=\sqrt{\frac{7}{70}}$化简为$\frac{\sqrt{7}}{\sqrt{70}}$，再代入$\sqrt{7}=a$，$\sqrt{70}=b$，得到$\frac{7a}{b}$，过程也正确。
所以两名同学的解法都正确。
$(2)$给出一种不同的解法
解：
因为$\sqrt{4.9}=\sqrt{\frac{490}{100}}=\frac{\sqrt{490}}{\sqrt{100}}=\frac{\sqrt{7×70}}{10}$，
又因为$\sqrt{7}=a$，$\sqrt{70}=b$，
根据二次根式乘法法则$\sqrt{mn}=\sqrt{m}\cdot\sqrt{n}$（$m\geq0,n\geq0$），则$\sqrt{7×70}=\sqrt{7}\cdot\sqrt{70}$，
所以$\sqrt{4.9}=\frac{\sqrt{7}\cdot\sqrt{70}}{10}=\frac{ab}{10}$。
还可以这样解：
$\sqrt{4.9}=\sqrt{\frac{7×70}{100}}=\frac{\sqrt{7}×\sqrt{70}}{10}$（根据$\sqrt{mn}=\sqrt{m}\cdot\sqrt{n}$，$m = 7,n = 70$以及$\sqrt{\frac{m}{n}}=\frac{\sqrt{m}}{\sqrt{n}}$，$m=7×70,n = 100$），
将$\sqrt{7}=a$，$\sqrt{70}=b$代入可得$\sqrt{4.9}=\frac{ab}{10}$。
另一种思路：
$\sqrt{4.9}=\sqrt{\frac{7^{2}×10}{10^{2}}}=\frac{7\sqrt{10}}{10}$，
因为$\sqrt{70}=\sqrt{7×10}=b$，则$\sqrt{10}=\frac{b}{a}$（$\sqrt{7}=a$），
所以$\sqrt{4.9}=\frac{7}{10}×\frac{b}{a}=\frac{7b}{10a}$。
综上，$(1)$ 两名同学解法都正确；$(2)$ $\sqrt{4.9}=\frac{7b}{10a}$（答案不唯一）。