第126页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
9. 【数学文化】我国南宋著名数学家秦九韶的著作《数书九章》里记载着这样一道题目:“问有沙田一块,有三斜,其中小斜五里,中斜十二里,大斜十三里,欲知为田几何?”其大意是:有一块三角形沙田,三条边长分别为 $ 5 $ 里、$ 12 $ 里、$ 13 $ 里,问这块沙田的面积有多大?题中“里”是我国市制长度单位,$ 1 $ 里 $ = 500 m $,则该沙田的面积为(
A.$ 7.5 km^{2} $
B.$ 15 km^{2} $
C.$ 75 km^{2} $
D.$ 750 km^{2} $
A
)A.$ 7.5 km^{2} $
B.$ 15 km^{2} $
C.$ 75 km^{2} $
D.$ 750 km^{2} $
答案:
9.A
10. [2023 济宁] 如图,在正方形方格中,每个小正方形的边长都是 $ 1 $ 个单位长度,点 $ A $,$ B $,$ C $,$ D $,$ E $ 均在小正方形方格的顶点上,线段 $ AB $,$ CD $ 相交于点 $ F $。若 $ \angle CFB = \alpha $,则 $ \angle ABE $ 等于(
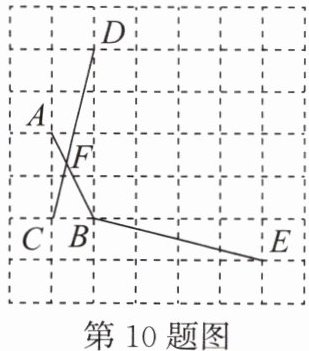
A.$ 180^{\circ}-\alpha $
B.$ 180^{\circ}-2\alpha $
C.$ 90^{\circ}+\alpha $
D.$ 90^{\circ}+2\alpha $
C
)
A.$ 180^{\circ}-\alpha $
B.$ 180^{\circ}-2\alpha $
C.$ 90^{\circ}+\alpha $
D.$ 90^{\circ}+2\alpha $
答案:
10.C
11. 如图,$ E $ 是正方形 $ ABCD $ 内的一点,连接 $ AE $,$ BE $,$ CE $,将 $ \triangle ABE $ 绕点 $ B $ 顺时针旋转 $ 90^{\circ} $ 到 $ \triangle CBE' $ 的位置。若 $ AE = 1 $,$ BE = 2 $,$ CE = 3 $,则 $ \angle BE'C = $
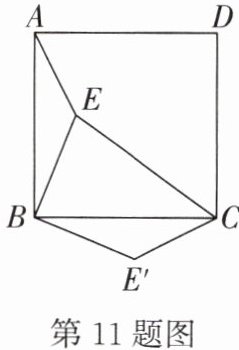
135^{\circ}
。
答案:
$11.135^{\circ}$
12. 古希腊的哲学家柏拉图曾指出,如果 $ m $ 是大于 $ 1 $ 的整数,$ a = 2m $,$ b = m^{2}-1 $,$ c = m^{2}+1 $,那么 $ a $,$ b $,$ c $ 为勾股数。你认为对吗?请说明理由。如果对,你能利用这个结论得出一些勾股数吗?
答案:
解:对。
理由如下:
已知$a = 2m$,$b = m^{2}-1$,$c = m^{2}+1$($m$是大于$1$的整数)。
计算$a^{2}+b^{2}$:
$a^{2}+b^{2}=(2m)^{2}+(m^{2} - 1)^{2}$
$=4m^{2}+m^{4}-2m^{2}+1$
$=m^{4}+2m^{2}+1$
计算$c^{2}$:
$c^{2}=(m^{2}+1)^{2}=m^{4}+2m^{2}+1$
所以$a^{2}+b^{2}=c^{2}$,满足勾股定理,$a$,$b$,$c$是勾股数。
当$m = 2$时,$a = 2×2 = 4$,$b = 2^{2}-1 = 3$,$c = 2^{2}+1 = 5$,即$3$,$4$,$5$是勾股数;
当$m = 3$时,$a = 2×3 = 6$,$b = 3^{2}-1 = 8$,$c = 3^{2}+1 = 10$,即$6$,$8$,$10$是勾股数;
当$m = 4$时,$a = 2×4 = 8$,$b = 4^{2}-1 = 15$,$c = 4^{2}+1 = 17$,即$8$,$15$,$17$是勾股数。(答案不唯一)
理由如下:
已知$a = 2m$,$b = m^{2}-1$,$c = m^{2}+1$($m$是大于$1$的整数)。
计算$a^{2}+b^{2}$:
$a^{2}+b^{2}=(2m)^{2}+(m^{2} - 1)^{2}$
$=4m^{2}+m^{4}-2m^{2}+1$
$=m^{4}+2m^{2}+1$
计算$c^{2}$:
$c^{2}=(m^{2}+1)^{2}=m^{4}+2m^{2}+1$
所以$a^{2}+b^{2}=c^{2}$,满足勾股定理,$a$,$b$,$c$是勾股数。
当$m = 2$时,$a = 2×2 = 4$,$b = 2^{2}-1 = 3$,$c = 2^{2}+1 = 5$,即$3$,$4$,$5$是勾股数;
当$m = 3$时,$a = 2×3 = 6$,$b = 3^{2}-1 = 8$,$c = 3^{2}+1 = 10$,即$6$,$8$,$10$是勾股数;
当$m = 4$时,$a = 2×4 = 8$,$b = 4^{2}-1 = 15$,$c = 4^{2}+1 = 17$,即$8$,$15$,$17$是勾股数。(答案不唯一)
13. 【跨学科融合·劳动教育】劳动教育能够提升学生的智力与创造力、强壮学生的体格。某实验中学为了给学生提供合适的劳动教育场地,在校园规划了一片劳动基地(四边形 $ ABCD $)用来种植蔬菜和花卉。如图,花卉区和蔬菜区之间用一条长 $ 13 m(AC = 13 m) $ 的小路隔开(小路的宽度忽略不计)。经测量,花卉区的 $ AB $ 边长 $ 5 m $,$ BC $ 边长 $ 12 m $,蔬菜区的 $ AD $ 边长 $ 7 m $,$ \angle D = 90^{\circ} $。
(1) 求蔬菜区边 $ CD $ 的长;
(2) 求花卉区的面积。
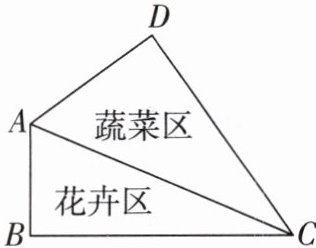
(1) 求蔬菜区边 $ CD $ 的长;
(2) 求花卉区的面积。

答案:
13.
(1)蔬菜区边CD的长为$20\sqrt{3}m (2)$花卉区的面积为$30m^{2}$
(1)蔬菜区边CD的长为$20\sqrt{3}m (2)$花卉区的面积为$30m^{2}$
14. 【几何直观】如图,$ P $ 是等边 $ \triangle ABC $ 内的一点,且 $ PA = 6 $,$ PB = 8 $,$ PC = 10 $,$ \angle PAP' = 60^{\circ} $,$ P'A = PA $,求 $ \angle APB $ 的度数。


答案:
1. 首先,连接$PP'$:
因为$\angle PAP' = 60^{\circ}$,$P'A = PA = 6$,根据等边三角形的判定定理(有一个角是$60^{\circ}$的等腰三角形是等边三角形),可知$\triangle APP'$是等边三角形。
所以$PP'=PA = 6$,$\angle APP' = 60^{\circ}$。
2. 然后,证明$\triangle AP'B\cong\triangle APC$:
因为$\triangle ABC$是等边三角形,所以$AB = AC$,$\angle BAC=\angle P'AP = 60^{\circ}$。
那么$\angle P'AB=\angle P'AP-\angle PAB$,$\angle PAC=\angle BAC - \angle PAB$,所以$\angle P'AB=\angle PAC$。
又因为$P'A = PA$,$AB = AC$,根据$SAS$(边角边)判定定理,可得$\triangle AP'B\cong\triangle APC$。
所以$P'B = PC = 10$。
3. 接着,在$\triangle P'PB$中:
已知$P'B = 10$,$PB = 8$,$PP' = 6$。
计算$PP'^{2}+PB^{2}$:$PP'^{2}+PB^{2}=6^{2}+8^{2}=36 + 64=100$,$P'B^{2}=10^{2}=100$。
所以$PP'^{2}+PB^{2}=P'B^{2}$。
根据勾股定理的逆定理(若$a^{2}+b^{2}=c^{2}$,则以$a$,$b$,$c$为边的三角形是直角三角形,其中$c$为斜边),可知$\triangle P'PB$是直角三角形,且$\angle P'PB = 90^{\circ}$。
4. 最后,求$\angle APB$的度数:
因为$\angle APB=\angle APP'+\angle P'PB$。
已知$\angle APP' = 60^{\circ}$,$\angle P'PB = 90^{\circ}$。
所以$\angle APB=60^{\circ}+90^{\circ}=150^{\circ}$。
综上,$\angle APB$的度数为$150^{\circ}$。
因为$\angle PAP' = 60^{\circ}$,$P'A = PA = 6$,根据等边三角形的判定定理(有一个角是$60^{\circ}$的等腰三角形是等边三角形),可知$\triangle APP'$是等边三角形。
所以$PP'=PA = 6$,$\angle APP' = 60^{\circ}$。
2. 然后,证明$\triangle AP'B\cong\triangle APC$:
因为$\triangle ABC$是等边三角形,所以$AB = AC$,$\angle BAC=\angle P'AP = 60^{\circ}$。
那么$\angle P'AB=\angle P'AP-\angle PAB$,$\angle PAC=\angle BAC - \angle PAB$,所以$\angle P'AB=\angle PAC$。
又因为$P'A = PA$,$AB = AC$,根据$SAS$(边角边)判定定理,可得$\triangle AP'B\cong\triangle APC$。
所以$P'B = PC = 10$。
3. 接着,在$\triangle P'PB$中:
已知$P'B = 10$,$PB = 8$,$PP' = 6$。
计算$PP'^{2}+PB^{2}$:$PP'^{2}+PB^{2}=6^{2}+8^{2}=36 + 64=100$,$P'B^{2}=10^{2}=100$。
所以$PP'^{2}+PB^{2}=P'B^{2}$。
根据勾股定理的逆定理(若$a^{2}+b^{2}=c^{2}$,则以$a$,$b$,$c$为边的三角形是直角三角形,其中$c$为斜边),可知$\triangle P'PB$是直角三角形,且$\angle P'PB = 90^{\circ}$。
4. 最后,求$\angle APB$的度数:
因为$\angle APB=\angle APP'+\angle P'PB$。
已知$\angle APP' = 60^{\circ}$,$\angle P'PB = 90^{\circ}$。
所以$\angle APB=60^{\circ}+90^{\circ}=150^{\circ}$。
综上,$\angle APB$的度数为$150^{\circ}$。
查看更多完整答案,请扫码查看


