第69页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
7. 在△ABC中,AD为边BC上的高,∠ABC=30°,∠CAD=20°,则∠BAC的度数是______.
答案:
7.80°或40°
8. 如图,分别过△ABC的顶点A,B作AD//BE.若∠CAD=25°,∠EBC=80°,则∠ACB的度数为(
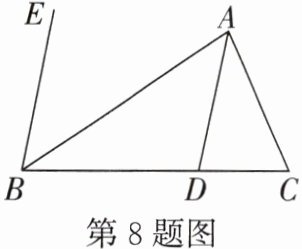
A.65°
B.75°
C.85°
D.95°
B
)
A.65°
B.75°
C.85°
D.95°
答案:
8.B
9. 【跨学科·物理】如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P,点F为焦点.若∠1=155°,∠2=30°,则∠3的度数为(

A.35°
B.45°
C.55°
D.65°
C
)
A.35°
B.45°
C.55°
D.65°
答案:
9.C
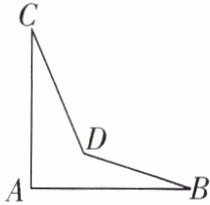
10. 一个零件的形状如图所示,按规定合格的零件标准为∠BAC=90°,∠B=21°,∠C=20°.检验工人量得∠BDC=130°,就断定这个零件不合格.你能运用所学的知识说出其中的道理吗?

答案:
解:延长$BD$交$AC$于点$E$。
根据三角形外角性质:三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABE$中,$\angle DEC$是$\triangle ABE$的外角,则$\angle DEC=\angle BAC + \angle B$。
已知$\angle BAC = 90^{\circ}$,$\angle B = 21^{\circ}$,所以$\angle DEC=90^{\circ}+21^{\circ}=111^{\circ}$。
在$\triangle DEC$中,$\angle BDC$是$\triangle DEC$的外角,则$\angle BDC=\angle DEC+\angle C$。
把$\angle DEC = 111^{\circ}$,$\angle C = 20^{\circ}$代入可得$\angle BDC=111^{\circ}+20^{\circ}=131^{\circ}$。
而检验工人量得$\angle BDC = 130^{\circ}\neq131^{\circ}$,所以这个零件不合格。
根据三角形外角性质:三角形的一个外角等于与它不相邻的两个内角之和。
在$\triangle ABE$中,$\angle DEC$是$\triangle ABE$的外角,则$\angle DEC=\angle BAC + \angle B$。
已知$\angle BAC = 90^{\circ}$,$\angle B = 21^{\circ}$,所以$\angle DEC=90^{\circ}+21^{\circ}=111^{\circ}$。
在$\triangle DEC$中,$\angle BDC$是$\triangle DEC$的外角,则$\angle BDC=\angle DEC+\angle C$。
把$\angle DEC = 111^{\circ}$,$\angle C = 20^{\circ}$代入可得$\angle BDC=111^{\circ}+20^{\circ}=131^{\circ}$。
而检验工人量得$\angle BDC = 130^{\circ}\neq131^{\circ}$,所以这个零件不合格。
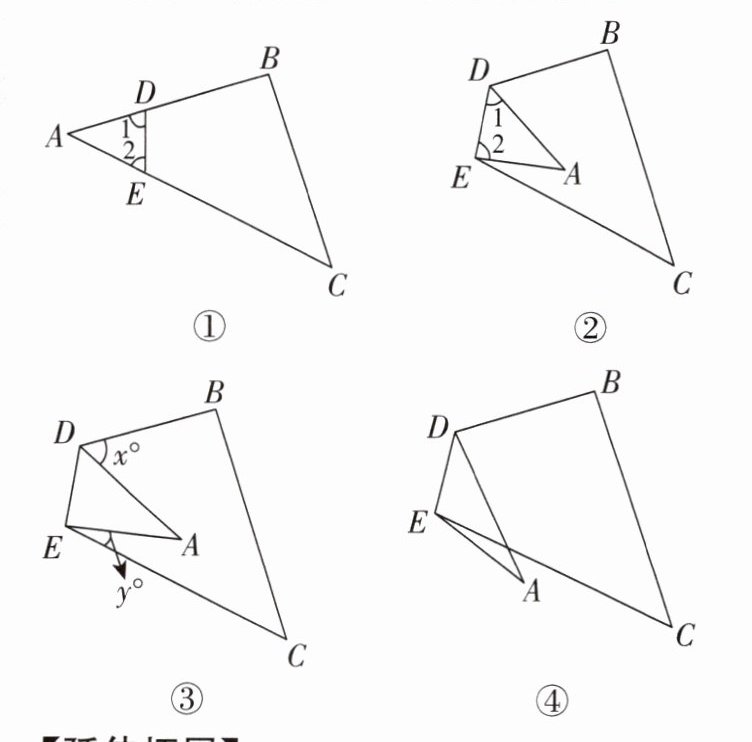
11. 【模型观念,推理能力】【问题背景】现有一张△ABC纸片,D,E分别是△ABC边AB,AC上的点.
【初步感知】(1)如图①,∠1+∠2与∠B+∠C存在怎样的数量关系?为什么?
(2)把图②的△ABC沿DE折叠,得到图②,填空:∠1+∠2_______∠B+∠C(填“>”“<”或“=”).
【深入探究】
(3)图③是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=_______.
(4)如图③,猜想∠BDA,∠CEA,∠A三个角存在的数量关系,并说明理由.
【延伸拓展】
(5)如图④,当点A落在△ABC的外侧时,探究∠BDA,∠CEA,∠A三个角存在的数量关系.(只要写出结论,不要求说明理由)
【初步感知】(1)如图①,∠1+∠2与∠B+∠C存在怎样的数量关系?为什么?
(2)把图②的△ABC沿DE折叠,得到图②,填空:∠1+∠2_______∠B+∠C(填“>”“<”或“=”).
【深入探究】
(3)图③是由图①的△ABC沿DE折叠得到的,如果∠A=30°,则x+y=_______.
(4)如图③,猜想∠BDA,∠CEA,∠A三个角存在的数量关系,并说明理由.

【延伸拓展】
(5)如图④,当点A落在△ABC的外侧时,探究∠BDA,∠CEA,∠A三个角存在的数量关系.(只要写出结论,不要求说明理由)
答案:
1. (1)
解:$\angle1+\angle2=\angle B + \angle C。$
理由:在$\triangle ABC$中,$\angle A+\angle B+\angle C = 180^{\circ}($三角形内角和定理:$\angle A+\angle B+\angle C=180^{\circ},$用\ \angle A+\angle B+\angle C = 180^{\circ}\表示),在$\triangle ADE$中,\angle A+\angle1+\angle2 = 180^{\circ}(\ \angle A+\angle1+\angle2 = 180^{\circ}\)。
所以$\angle1+\angle2=\angle B+\angle C($等量代换)。
2. (2)
答案:=。
理由:因为$\angle A+\angle B+\angle C = 180^{\circ},$$\angle A+\angle1+\angle2 = 180^{\circ}($折叠前后角的大小不变,$\angle A$不变),所以$\angle1+\angle2=\angle B+\angle C。$
3. (3)
答案:$60^{\circ}。$
理由:由(1)知$\angle1+\angle2=\angle B+\angle C,$又因为$\angle A = 30^{\circ},$$\angle A+\angle B+\angle C = 180^{\circ},$所以$\angle B+\angle C=180^{\circ}-\angle A = 150^{\circ},$$\angle1+\angle2 = 150^{\circ}。$
又因为$x + y+(\angle1+\angle2)=360^{\circ}-2(\angle B+\angle C)($周角$360^{\circ},$\x + y+(\angle1+\angle2)=360^{\circ}\,折叠后$\angle ADE=\angle A'DE,$$\angle AED=\angle A'ED),$$x + y=360^{\circ}-(\angle1+\angle2)-2(\angle B+\angle C),$$x + y=360^{\circ}-(180^{\circ}-\angle A)-2(180^{\circ}-\angle A),$把$\angle A = 30^{\circ}$代入得$x + y = 60^{\circ}。$4. (4) - 解:$\angle BDA+\angle CEA = 2\angle A。$ - 理由:设$\angle ADE=\angle A'DE = m,$$\angle AED=\angle A'ED = n。$ - 则$\angle BDA = 180^{\circ}-2m,$$\angle CEA = 180^{\circ}-2n。$ - 所以$\angle BDA+\angle CEA=360^{\circ}-2(m + n)。$ - 在$\triangle ADE$中,$m + n=180^{\circ}-\angle A。$ - 所以$\angle BDA+\angle CEA=360^{\circ}-2(180^{\circ}-\angle A)=2\angle A。$5. (5) - 答案:$\angle BDA-\angle CEA = 2\angle A。$ - 理由:设$\angle ADE=\angle A'DE = m,$$\angle AED=\angle A'ED = n。$ - 则$\angle BDA = 180^{\circ}-2m,$$\angle CEA=2n - 180^{\circ}。$$ - \angle BDA-\angle CEA=(180^{\circ}-2m)-(2n - 180^{\circ})=360^{\circ}-2(m + n),$又$m + n = 180^{\circ}-\angle A,$所以$\angle BDA-\angle CEA=2\angle A。$
解:$\angle1+\angle2=\angle B + \angle C。$
理由:在$\triangle ABC$中,$\angle A+\angle B+\angle C = 180^{\circ}($三角形内角和定理:$\angle A+\angle B+\angle C=180^{\circ},$用\ \angle A+\angle B+\angle C = 180^{\circ}\表示),在$\triangle ADE$中,\angle A+\angle1+\angle2 = 180^{\circ}(\ \angle A+\angle1+\angle2 = 180^{\circ}\)。
所以$\angle1+\angle2=\angle B+\angle C($等量代换)。
2. (2)
答案:=。
理由:因为$\angle A+\angle B+\angle C = 180^{\circ},$$\angle A+\angle1+\angle2 = 180^{\circ}($折叠前后角的大小不变,$\angle A$不变),所以$\angle1+\angle2=\angle B+\angle C。$
3. (3)
答案:$60^{\circ}。$
理由:由(1)知$\angle1+\angle2=\angle B+\angle C,$又因为$\angle A = 30^{\circ},$$\angle A+\angle B+\angle C = 180^{\circ},$所以$\angle B+\angle C=180^{\circ}-\angle A = 150^{\circ},$$\angle1+\angle2 = 150^{\circ}。$
又因为$x + y+(\angle1+\angle2)=360^{\circ}-2(\angle B+\angle C)($周角$360^{\circ},$\x + y+(\angle1+\angle2)=360^{\circ}\,折叠后$\angle ADE=\angle A'DE,$$\angle AED=\angle A'ED),$$x + y=360^{\circ}-(\angle1+\angle2)-2(\angle B+\angle C),$$x + y=360^{\circ}-(180^{\circ}-\angle A)-2(180^{\circ}-\angle A),$把$\angle A = 30^{\circ}$代入得$x + y = 60^{\circ}。$4. (4) - 解:$\angle BDA+\angle CEA = 2\angle A。$ - 理由:设$\angle ADE=\angle A'DE = m,$$\angle AED=\angle A'ED = n。$ - 则$\angle BDA = 180^{\circ}-2m,$$\angle CEA = 180^{\circ}-2n。$ - 所以$\angle BDA+\angle CEA=360^{\circ}-2(m + n)。$ - 在$\triangle ADE$中,$m + n=180^{\circ}-\angle A。$ - 所以$\angle BDA+\angle CEA=360^{\circ}-2(180^{\circ}-\angle A)=2\angle A。$5. (5) - 答案:$\angle BDA-\angle CEA = 2\angle A。$ - 理由:设$\angle ADE=\angle A'DE = m,$$\angle AED=\angle A'ED = n。$ - 则$\angle BDA = 180^{\circ}-2m,$$\angle CEA=2n - 180^{\circ}。$$ - \angle BDA-\angle CEA=(180^{\circ}-2m)-(2n - 180^{\circ})=360^{\circ}-2(m + n),$又$m + n = 180^{\circ}-\angle A,$所以$\angle BDA-\angle CEA=2\angle A。$
查看更多完整答案,请扫码查看


