第118页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
5. 如图,在$\triangle ABC$中,$AB = AC$,$AD$是$\angle BAC$的平分线。已知$AB = 13,BC = 24$,则$AD$的长为
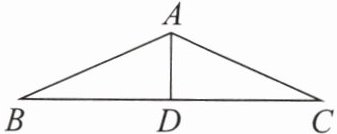
5
。
答案:
5. 5
6. 在$Rt\triangle ABC$中,$\angle C = 90^{\circ}$,且$\angle A,\angle B,\angle C$的对应边分别为$a,b,c$。
(1)已知$c = 25,b = 15$,求$a$的长;
(2)已知$a = 7,b = 24$,求$c$的长;
(3)已知$a:b = 1:3$,且$c = 10$,求$a,b$的长。
(1)已知$c = 25,b = 15$,求$a$的长;
(2)已知$a = 7,b = 24$,求$c$的长;
(3)已知$a:b = 1:3$,且$c = 10$,求$a,b$的长。
答案:
6.
(1)$a = 20$
(2)$c = 25$
(3)$a = \sqrt{10},b = 3\sqrt{10}$
(1)$a = 20$
(2)$c = 25$
(3)$a = \sqrt{10},b = 3\sqrt{10}$
7. 【数学文化】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展。现用四个全等的直角三角形拼成如图所示的“弦图”。在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ},AC = b,BC = a,AB = c$。求证:$a^{2}+b^{2} = c^{2}$。
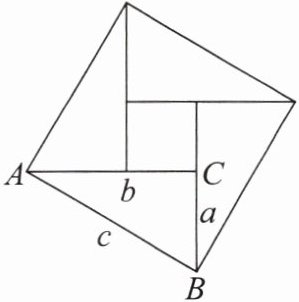

答案:
解:大正方形的面积可以表示为$c^{2}$。
大正方形的面积也可以表示为四个全等直角三角形的面积与中间小正方形面积之和。
四个直角三角形的面积为$4×\frac{1}{2}ab = 2ab$,中间小正方形的边长为$(b - a)$,其面积为$(b - a)^{2}$。
所以大正方形面积又可表示为$2ab+(b - a)^{2}$。
则$c^{2}=2ab+(b - a)^{2}$
展开$(b - a)^{2}$得$c^{2}=2ab + b^{2}-2ab + a^{2}$
化简可得$a^{2}+b^{2}=c^{2}$。
综上,$a^{2}+b^{2}=c^{2}$得证。
大正方形的面积也可以表示为四个全等直角三角形的面积与中间小正方形面积之和。
四个直角三角形的面积为$4×\frac{1}{2}ab = 2ab$,中间小正方形的边长为$(b - a)$,其面积为$(b - a)^{2}$。
所以大正方形面积又可表示为$2ab+(b - a)^{2}$。
则$c^{2}=2ab+(b - a)^{2}$
展开$(b - a)^{2}$得$c^{2}=2ab + b^{2}-2ab + a^{2}$
化简可得$a^{2}+b^{2}=c^{2}$。
综上,$a^{2}+b^{2}=c^{2}$得证。
8. 若直角三角形的三边长分别为$2,4,x$,则$x$的值为(
A.$3$
B.$2\sqrt{5}$
C.$2\sqrt{3}$
D.$2\sqrt{5}$或$2\sqrt{3}$
D
)A.$3$
B.$2\sqrt{5}$
C.$2\sqrt{3}$
D.$2\sqrt{5}$或$2\sqrt{3}$
答案:
8. D
9. 如图,以$Rt\triangle ABC$的三边为直径分别向外作半圆,若斜边$AB = 3$,则图中阴影部分的面积为(
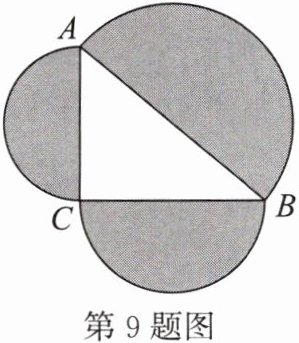
A.$9\pi$
B.$\frac{9}{2}\pi$
C.$\frac{9}{4}\pi$
D.$3\pi$
C
)
A.$9\pi$
B.$\frac{9}{2}\pi$
C.$\frac{9}{4}\pi$
D.$3\pi$
答案:
9. C
10. 【教材P167“议一议”改编】如图,数轴上的点$O$表示的数是$0$,点$A$表示的数是$2$,$OB\perp OA$,垂足为$O$,且$OB = 1$,以点$A$为圆心,$AB$长为半径画弧,交数轴于点$C$,则点$C$表示的数为(
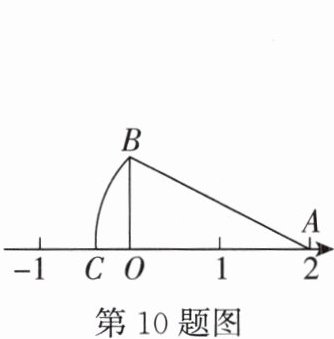
A.$2-\sqrt{3}$
B.$-2+\sqrt{5}$
C.$2-\sqrt{5}$
D.$-2+\sqrt{3}$
C
)
A.$2-\sqrt{3}$
B.$-2+\sqrt{5}$
C.$2-\sqrt{5}$
D.$-2+\sqrt{3}$
答案:
10. C
11. 【数学文化】[2024眉山]如图,图①是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成。若图①中大正方形的面积为$24$,小正方形的面积为$4$,现将这四个直角三角形拼成图②,则图②中大正方形的面积为(
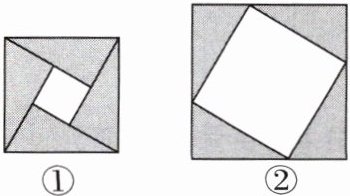
A.$24$
B.$36$
C.$40$
D.$44$
D
)
A.$24$
B.$36$
C.$40$
D.$44$
答案:
11. D
查看更多完整答案,请扫码查看


