第91页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
9. (1) (2025·编写) 当 $ x = 6 $,$ y = 4 $ 时,求下列各代数式的值:
① $ (x + y)(x - y) $;
② $ x^2 + 2xy + y^2 $。
(2) (2025·编写) 当 $ x = 20 $ 时,代数式 $ ax^3 + bx - 7 $ 的值为 9;当 $ x = -20 $ 时,求代数式 $ ax^3 + bx + 2 $ 的值。
① $ (x + y)(x - y) $;
② $ x^2 + 2xy + y^2 $。
(2) (2025·编写) 当 $ x = 20 $ 时,代数式 $ ax^3 + bx - 7 $ 的值为 9;当 $ x = -20 $ 时,求代数式 $ ax^3 + bx + 2 $ 的值。
答案:
9.
(1)【解】①将x=6,y=4代入(x+y)(x-y),得原式=(6+4)×(6-4)=10×2=20.②将x=6,y=4代入$x^{2}+2xy+y^{2}$,得原式=$6^{2}+2×6×4+4^{2}=36+48+16=100$.
(2)【解】由题意,得当x=20时,$20^{3}a+20b=16$,则当x=-20时,得$-20^{3}a-20b=-16$,所以$-20^{3}a-20b+2=-14$.
(1)【解】①将x=6,y=4代入(x+y)(x-y),得原式=(6+4)×(6-4)=10×2=20.②将x=6,y=4代入$x^{2}+2xy+y^{2}$,得原式=$6^{2}+2×6×4+4^{2}=36+48+16=100$.
(2)【解】由题意,得当x=20时,$20^{3}a+20b=16$,则当x=-20时,得$-20^{3}a-20b=-16$,所以$-20^{3}a-20b+2=-14$.
10. (1) (2025·编写) 某地出租车按实际租车里程收租车费,该地规定不足 3 千米统一收租车费 10 元,超过 3 千米 (含 3 千米) 后每超 1 千米加收租车费 2.4 元。
① 若某人乘出租车 $ x $ 千米,则租车费是多少元?
② 若小明乘出租车的租车费为 18.4 元,则他实际租车里程为多少千米?
(2) (2025·简阳) 当 $ x = 1 $ 时,式子 $ 5ax^3 + 3bx + 9 $ 的值为 4。当 $ x = -1 $ 时,求式子 $ 5ax^3 + 3bx + 9 $ 的值。
① 若某人乘出租车 $ x $ 千米,则租车费是多少元?
② 若小明乘出租车的租车费为 18.4 元,则他实际租车里程为多少千米?
(2) (2025·简阳) 当 $ x = 1 $ 时,式子 $ 5ax^3 + 3bx + 9 $ 的值为 4。当 $ x = -1 $ 时,求式子 $ 5ax^3 + 3bx + 9 $ 的值。
答案:
10.
(1)【解】①当x<3时,应付车费是10元;当x≥3且为整数,应付车费:$10+(x-3)×2.4=$(2.4x+2.8)元.②设他实际租车里程为a千米.根据题意,得10+(a-3)×2.4=18.4,解得a=6.5.即他实际租车里程为6.5千米.
(2)【解】当x=1时,$5ax^{3}+3bx+9=5a+3b+9=4$,
∴5a+3b=-5,
∴当x=-1时,$5ax^{3}+3bx+9=-5a-3b+9=-(5a+3b)+9=-(-5)+9=14$.
(1)【解】①当x<3时,应付车费是10元;当x≥3且为整数,应付车费:$10+(x-3)×2.4=$(2.4x+2.8)元.②设他实际租车里程为a千米.根据题意,得10+(a-3)×2.4=18.4,解得a=6.5.即他实际租车里程为6.5千米.
(2)【解】当x=1时,$5ax^{3}+3bx+9=5a+3b+9=4$,
∴5a+3b=-5,
∴当x=-1时,$5ax^{3}+3bx+9=-5a-3b+9=-(5a+3b)+9=-(-5)+9=14$.
11. (2024·简阳) 若 $ x $,$ y $ 互为相反数,$ a $,$ b $ 互为倒数,$ |n| = 2 $,则 $ 5x + 5y - \frac{3ab}{n^3} = $______。
答案:
$-\frac{3}{8}$或$\frac{3}{8}$
12. (2025·锦江) 已知 $ a = 3b - 4 $,则代数式 $ 9b - 3a + 2024 $ 的值为______。
答案:
2036
13. (2025·锦江) 下表是小明同学探究关于 $ x $ 的代数式 $ |ax| + b $ (其中 $ a $,$ b $ 为常数) 的值变化规律的情况,则 $ |2025a| + b = $______。
| $ x $ | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| $ |ax| + b $ | -1 | -4 | -7 | -10 | -7 | -4 | -1 |
| $ x $ | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| $ |ax| + b $ | -1 | -4 | -7 | -10 | -7 | -4 | -1 |
答案:
6065
14. (1) (2025·简阳) 人在运动时的心跳速率通常和人的年龄有关。如果用 $ a $ 表示一个人的年龄,用 $ b $ 表示正常情况下这个人在运动时所能承受的每分钟心跳的最高次数,那么 $ b = 0.8(220 - a) $。
① 正常情况下,一个 14 岁的少年在运动时所能承受的每分钟心跳的最高次数是多少?
② 一个 45 岁的人运动时 10 s 心跳的次数为 22 次,他有危险吗?请说明理由。
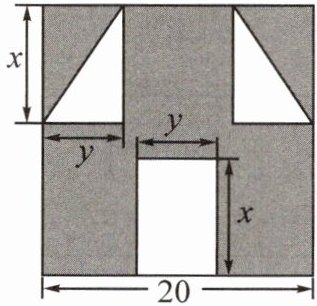
(2) (2024·青羊) 网络流行语“囧”,像一个人脸郁闷的神情。如图所示,一张边长为 20 的正方形的纸片,剪去两个相同的小直角三角形和一个长方形得到一个“囧”字图案 (阴影部分)。设剪去的小长方形长和宽分别为 $ x $,$ y $,剪去的两个小直角三角形的两直角边长也分别为 $ x $,$ y $。
① 用含有 $ x $,$ y $ 的代数式表示图中“囧”的面积;
② 当 $ x = 8 $,$ y = 4 $ 时,求此时“囧”的面积。
① 正常情况下,一个 14 岁的少年在运动时所能承受的每分钟心跳的最高次数是多少?
② 一个 45 岁的人运动时 10 s 心跳的次数为 22 次,他有危险吗?请说明理由。
(2) (2024·青羊) 网络流行语“囧”,像一个人脸郁闷的神情。如图所示,一张边长为 20 的正方形的纸片,剪去两个相同的小直角三角形和一个长方形得到一个“囧”字图案 (阴影部分)。设剪去的小长方形长和宽分别为 $ x $,$ y $,剪去的两个小直角三角形的两直角边长也分别为 $ x $,$ y $。
① 用含有 $ x $,$ y $ 的代数式表示图中“囧”的面积;
② 当 $ x = 8 $,$ y = 4 $ 时,求此时“囧”的面积。

答案:
14.
(1)【解】①由题意知,b=0.8(220-a),当a=14时,b=0.8×(220-14)≈164(次).即正常情况下,一个14岁的少年在运动时所能承受的每分钟心跳的最高次数约为164.②正常情况下无危险.理由如下:当a=45时,b=0.8×(220-45)=140.
∵22×(60÷10)=132,132<140,
∴他没有危险.
(2)【解】①由题意可知,剪去的两个直角三角形和一个长方形的面积和=2xy,
∴"囧"的面积=20×20-2xy=400-2xy.②当x=8,y=4时,400-2xy=400-2×8×4=336,
∴"囧"的面积为336.
(1)【解】①由题意知,b=0.8(220-a),当a=14时,b=0.8×(220-14)≈164(次).即正常情况下,一个14岁的少年在运动时所能承受的每分钟心跳的最高次数约为164.②正常情况下无危险.理由如下:当a=45时,b=0.8×(220-45)=140.
∵22×(60÷10)=132,132<140,
∴他没有危险.
(2)【解】①由题意可知,剪去的两个直角三角形和一个长方形的面积和=2xy,
∴"囧"的面积=20×20-2xy=400-2xy.②当x=8,y=4时,400-2xy=400-2×8×4=336,
∴"囧"的面积为336.
查看更多完整答案,请扫码查看


