《2025年天府前沿七年级数学上册北师大版》

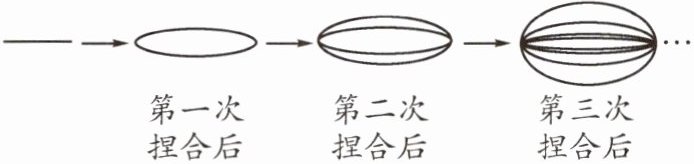
12. (2025·青羊)你喜欢吃拉面吗？拉面馆的师傅,用一根很粗的面条,把两头捏合在一起拉伸,再捏合,再拉伸,反复几次,就把这根很粗的面条拉成了许多细的面条,如图所示,这样捏合到第____次后可拉出256根面条。

答案： 8

13. (2025·简阳)下列说法：①若$x^{2} = 1$,则$x = \pm1$；②单项式$-2^{2}ab^{2}和多项式x^{3} + x^{2}$都是五次整式；③若$a + b + c\gt0,abc\lt0$,则$\frac{|a|}{a}-\frac{b}{|b|}+\frac{|c|}{c}-\frac{|abc|}{abc}$的结果有两个；④若$2(ax^{2} - x + 2)-(4x^{2} + 5x + a)的运算结果中不含x^{2}$项,则常数项为2.其中一定正确的结论是____。(填序号)

答案： ①③④

14. (2024·青羊)一般情况下,等式$\frac{x}{3}+\frac{y}{4}= \frac{x + y}{3 + 4}$不成立,但有些数可以使它成立,如$x = y = 0$。我们称使等式$\frac{x}{3}+\frac{y}{4}= \frac{x + y}{3 + 4}成立的一对数x,y$为“互制数对”,记为$[x,y]$。
(1)若$[1,a]$是“互制数对”,求$a$的值；
(2)若$[m,n]$是“互制数对”,求代数式$m - \frac{22}{3}n - [\frac{19}{3}m - \frac{13}{3}(n - 3)]$的值。

答案： 【解】
(1)$\because [1,a]$是"互制数对",$\therefore \frac{1}{3}+\frac{a}{4}=\frac{1+a}{3+4}$,解得$a=-\frac{16}{9}$.
(2)$\because [m,n]$是"互制数对",$\therefore \frac{m}{3}+\frac{n}{4}=\frac{m+n}{3+4}$,$\therefore 16m=-9n$,$\therefore m-\frac{22}{3}n-[\frac{19}{3}m-\frac{13}{3}(n-3)]=m-\frac{22}{3}n-\frac{19}{3}m+\frac{13}{3}n-13=-\frac{16}{3}m-3n-13=3n-3n-13=-13$.

15. (2024·郫都)已知有理数$a,b,c在数轴上对应的点分别为A,B,C$,且满足$(a - 1)^{2} + |ab + 3| = 0,c = -2a + b$。
(1)分别求$a,b,c$的值。
(2)若点$D在数轴上对应的数为x$,当$A,D间距离是B,C$间距离的4倍时,请求出$x$的值。
(3)若点$A和点B$分别以每秒2个单位长度和每秒1个单位长度的速度在数轴上同时向右运动,设运动时间为$t$秒,是否存在一个常数$k$,使得$3AC - kAB的值在一定时间范围内不随运动时间t$的改变而改变？若存在,求出$k$的值；若不存在,请说明理由。

答案： 【解】
(1)$\because (a-1)^{2}\geq0$,$|ab+3|\geq0$,$(a-1)^{2}+|ab+3|=0$,$\therefore a-1=0,ab+3=0$,$\therefore a=1,b=-3$.又$\because c=-2a+b$,$\therefore c=-2×1+(-3)=-5$.
(2)由题意,得$|x-1|=4×(-3+5)$,$\therefore x-1=\pm8$.当$x-1=8$时,$x=9$;当$x-1=-8$时,$x=-7$,综上所述,$x=9$或$-7$.
(3)假设存在符合条件的k,经过t秒,点A表示的数为$1+2t$,点B表示的数为$-3+t$,且A,B都在点C右侧,$\therefore AC=1+2t-(-5)=6+2t$,$AB=1+2t-(-3+t)=4+t$,$\therefore 3AC-kAB=3(6+2t)-k(4+t)=18+6t-4k-kt=18-4k+(6-k)t$.$\because$3AC-kAB的值在一定时间范围内不随运动时间t的改变而改变,$\therefore 6-k=0$,$\therefore k=6$,$\therefore$存在符合条件的k,$k=6$.