《2025年天府前沿七年级数学上册北师大版》

11. (1)(2025·编写)若$|x|= 3$,$y^{2}= 4$,且$y＞x$,则$x+y= $____.
(2)(2025·编写)有下列各数：①$-|-(-5)|$,②$-[-(-7)]$,③$-(-5)^{4}$,④$(-11)^{2}$,其中运算结果为负数的有____个.

答案：
(1)-1或-5；
(2)3

12. (2025·东部新区)计算：$2^{1}-1= 1$,$2^{2}-1= 3$,$2^{3}-1= 7$,$2^{4}-1= 15$,$2^{5}-1= 31$,…$$.归纳各计算结果中的个位数字规律,猜测$2^{2026}-1$的个位数字是____.

答案： 3

13. (1)(2025·编写)计算：$(-1)^{2023}×(-\frac {2}{3})^{2024}×1.5^{2025}= $____.
(2)(2025·编写)若$2^{n}-1= 5$,则$4×2^{n}-4= $____.

答案：
(1)$-\frac{3}{2}$；
(2)20

14. (2025·编写)超市推出如下优惠方案：
①一次性购物不超过$100$元,不享受优惠；②一次性购物超过$100$元,但不超过$300$元,一律九折；③一次性购物超过$300$元,一律八折.
某人两次购物分别付款$80$元、$252$元,如果他将这两次所购商品一次性购买,求实际应付款多少元.

答案： 【解】当252元的商品的实际价值在300元以下(包括300元)时,它的实际价值为$252÷0.9=280$(元),故应付款$(280+80)×0.8=288$(元);
当252元的商品的实际价值在300元以上时,它的实际价值为$252÷0.8=315$(元),故应付款$(315+80)×0.8=316$(元).
故实际应付款288元或316元.

15. (2025·编写)如图,已知数轴上的两点$A$,$B对应的数分别为-1$,$3$,$P$为数轴上的一动点,其对应的数为$x$.
＜image＞＜/image＞

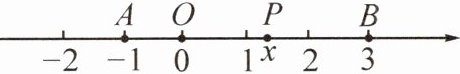
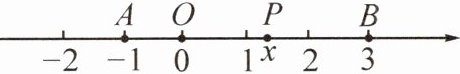
(1)若点$P到点A$,$B$的距离相等,求点$P$对应的数.
(2)数轴上是否存在点$P$,使点$P到点A$,$B的距离之和为6$个单位长度？若存在,请求出$x$的值；若不存在,请说明理由.
(3)点$A$,$B分别以2$个单位长度/分、$1$个单位长度/分的速度向右运动,同时点$P以6$个单位长度/分的速度从点$O$向左运动.当遇到点$A$时,点$P$立即以同样的速度向右运动,并不停地往返于点$A与点B$之间.当点$A与点B$重合时,点$P$所经过的总路程是多少？

答案： 【解】
(1)因为$PA=PB$,所以$|x-(-1)|=|3-x|$,所以$x=1$,所以点P对应的数为1.
(2)存在.理由如下:
因为$PA+PB=6$个单位长度,
所以$|x-(-1)|+|x-3|=6$,
解得$x=-2$或$x=4$.
(3)设点A追上点B所用的时间为t分钟,则$2t-t=3-(-1)$,解得$t=4$,
所以点P所经过的总路程为$4×6=24$(个)单位长度.