第134页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
- 第137页
- 第138页
- 第139页
- 第140页
- 第141页
- 第142页
- 第143页
- 第144页
- 第145页
- 第146页
- 第147页
- 第148页
- 第149页
- 第150页
- 第151页
- 第152页
- 第153页
- 第154页
- 第155页
- 第156页
- 第157页
- 第158页
- 第159页
- 第160页
- 第161页
- 第162页
- 第163页
12. (2025·编写)已知∠AOB= $100^{\circ}$,射线OC在同一平面内绕点O旋转,射线OE,OF分别是∠AOC和∠COB的平分线,则∠EOF的度数为______.
答案:
50°或130°
13. (2024·青羊)某人下午6点多钟外出购物,表上时针和分针的夹角恰好是$110^{\circ}$,将近7点钟回到家,此时,表上时针和分针的夹角又恰好是$110^{\circ}$,则此人外出购物所用时间是______分钟.
答案:
40
14. (2024·武侯)在直线AB上任取一点O,过点O作射线OC,OD,使∠COD= $90^{\circ}$,当∠AOC= $50^{\circ}$时,求∠BOD的度数.
答案:
[解]如图,当射线OC,OD在直线AB的同一侧时,
∵∠COD=90°,
∴∠BOD=180°−90°−∠AOC=180°−90°−50°=40°.当射线OC,OD在直线AB的两侧时,
∵∠COD=90°,
∴∠AOD=90°−∠AOC=90°−50°=40°,
∴∠BOD=180°−∠AOD=180°−40°=140°.综上所述,∠BOD的度数是40°或140°.
∵∠COD=90°,
∴∠BOD=180°−90°−∠AOC=180°−90°−50°=40°.当射线OC,OD在直线AB的两侧时,
∵∠COD=90°,
∴∠AOD=90°−∠AOC=90°−50°=40°,
∴∠BOD=180°−∠AOD=180°−40°=140°.综上所述,∠BOD的度数是40°或140°.
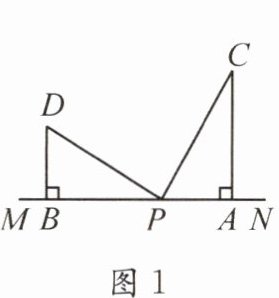
15. (2025·天府新区)如图,两个形状、大小完全相同的含有$30^{\circ}$,$60^{\circ}$角的三角板如图1所示放置,PA,PB与直线MN重合,且三角板PAC,三角板PBD均可绕点P逆时针旋转.
(1)试说明图1中∠DPC= $90^{\circ}$.
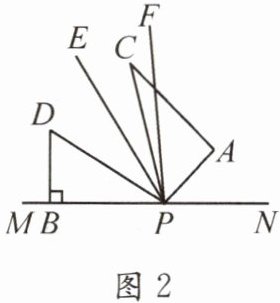
(2)如图2,若三角板PAC的边PA从PN处开始绕点P按逆时针方向旋转一定度数,PF平分∠APD,PE平分∠CPD,求∠EPF的度数.
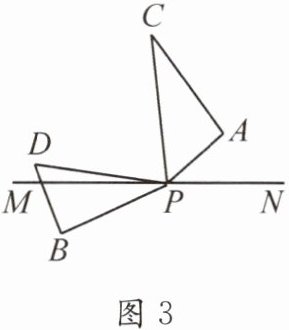
(3)如图3,若三角板PAC的边PA从PN处开始绕点P按逆时针方向旋转,转速为$5^{\circ}/s$,同时三角板PBD的边PB从PM处开始绕点P按逆时针方向旋转,转速为$3^{\circ}/s$,在两个三角形旋转过程中(PC转到与PM重合时,两个三角板都停止转动),问是否存在某个时刻,使∠BPN:∠CPD= 9:4,若存在,请求出t的值;若不存在,请说明理由.
(1)试说明图1中∠DPC= $90^{\circ}$.
(2)如图2,若三角板PAC的边PA从PN处开始绕点P按逆时针方向旋转一定度数,PF平分∠APD,PE平分∠CPD,求∠EPF的度数.
(3)如图3,若三角板PAC的边PA从PN处开始绕点P按逆时针方向旋转,转速为$5^{\circ}/s$,同时三角板PBD的边PB从PM处开始绕点P按逆时针方向旋转,转速为$3^{\circ}/s$,在两个三角形旋转过程中(PC转到与PM重合时,两个三角板都停止转动),问是否存在某个时刻,使∠BPN:∠CPD= 9:4,若存在,请求出t的值;若不存在,请说明理由.



答案:
[解]
(1)由题意,得∠CPA=60°,∠DPB=30°,则∠DPC=∠BPA−∠CPA−∠DPB=180°−60°−30°=90°.
(2)
∵PE平分∠CPD,
∴可设∠CPE=∠DPE=x,∠CPF=y.则∠APF=60°−y,∠DPF=2x+y
∵PE平分∠APD,
∴y+2x=60°−y,
∴x+y=30°,
∴∠EPF=∠CPE+∠CPF=x+y=30°,即∠EPF的度数为30°.
(3)在旋转过程中,存在某个时刻,使∠BPN:∠CPD=9:4.设运动时间为t秒,
∴∠CPD=90°−5t°+3t°=90°−2t°,∠BPN=180°−∠BPM=180°−3t°,
∴$\frac{180°−3t°}{90°−2t°}$=$\frac{9}{4}$,解得t=15,故存在某个时刻,使∠BPN:∠CPD=9:4,此时,t=15.
(1)由题意,得∠CPA=60°,∠DPB=30°,则∠DPC=∠BPA−∠CPA−∠DPB=180°−60°−30°=90°.
(2)
∵PE平分∠CPD,
∴可设∠CPE=∠DPE=x,∠CPF=y.则∠APF=60°−y,∠DPF=2x+y
∵PE平分∠APD,
∴y+2x=60°−y,
∴x+y=30°,
∴∠EPF=∠CPE+∠CPF=x+y=30°,即∠EPF的度数为30°.
(3)在旋转过程中,存在某个时刻,使∠BPN:∠CPD=9:4.设运动时间为t秒,
∴∠CPD=90°−5t°+3t°=90°−2t°,∠BPN=180°−∠BPM=180°−3t°,
∴$\frac{180°−3t°}{90°−2t°}$=$\frac{9}{4}$,解得t=15,故存在某个时刻,使∠BPN:∠CPD=9:4,此时,t=15.
查看更多完整答案,请扫码查看


