《2025年超越训练八年级数学上册人教版四川专版》

12. 先化简, 再求值: $(x + y)(x - y)+(x - y)^{2}-(6x^{2}y - 2xy^{2})÷(2y)$, 其中 $x$, $y$ 满足 $(x + 2)^{2}+|y - 1|=0$.

答案： 12.解：原式=$-x^{2}-xy$.$\because(x + 2)^{2}+|y - 1|=0$,$\therefore x = - 2$,$y=1$.当$x = - 2$,$y = 1$时，原式=$-(-2)^{2}-(-2)×1=-2$.

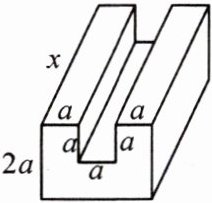
13. 一个工件的形状和部分尺寸如图所示, 其体积为 $a(a + 1)(5a + 1)+(3a + 2)(3a - 2)-a + 4$, 求工件的长 $x$ 是多少 (用含 $a$ 的式子表示).

答案： 13.解：由题图可得此工件的横截面的面积为$2a\cdot3a - a^{2}=5a^{2}$.此工件的体积为$a(a + 1)(5a + 1)+(3a + 2)(3a - 2)-a + 4=a(5a^{2}+6a + 1)+9a^{2}-4 - a + 4=5a^{3}+6a^{2}+a + 9a^{2}-4 -a + 4=5a^{3}+15a^{2}$.由题意，得$x=(5a^{3}+15a^{2})÷(5a^{2})=a + 3$，即此工件的长$x$是$a + 3$.

14. 观察下列各式:
$(x^{2}-1)÷(x - 1)=x + 1$;
$(x^{3}-1)÷(x - 1)=x^{2}+x + 1$;
$(x^{4}-1)÷(x - 1)=x^{3}+x^{2}+x + 1$;
$(x^{5}-1)÷(x - 1)=x^{4}+x^{3}+x^{2}+x + 1$;
……
(1) 根据规律, 你能得到一般情况下 $(x^{n}-1)÷(x - 1)$ ($n$ 是不小于 $2$ 的整数) 的结果吗?
(2) 根据这一结果计算: $1 + 2 + 2^{2}+2^{3}+…+2^{2022}+2^{2023}+2^{2024}+2^{2025}$.
(3) 若 $1 + x + x^{2}+…+x^{2024}=0$, 求 $x^{2025}$ 的值.

答案： 14.解：
(1)$(x^{n}-1)÷(x - 1)=x^{n - 1}+x^{n - 2}+\cdots+x + 1$.
(2)$1+2+2^{2}+2^{3}+\cdots+2^{2022}+2^{2023}+2^{2024}+2^{2025}=(2^{2026}-1)÷(2 - 1)=2^{2026}-1$.
(3)$\because1 + x+x^{2}+\cdots+x^{2024}=0$,$\therefore x^{2025}-1=0$,$\therefore x^{2025}=1$.

15. 阅读材料:
因为 $(x + 3)(x - 2)=x^{2}+x - 6$, 所以 $(x^{2}+x - 6)÷(x - 2)=x + 3$. 这说明 $x^{2}+x - 6$ 能被 $x - 2$ 整除, 同时也说明多项式 $x^{2}+x - 6$ 有一个因式为 $x - 2$, 另外当 $x = 2$ 时, 多项式 $x^{2}+x - 6$ 的值为 $0$.
问题解决:
(1) 已知 $x - 2$ 能整除 $x^{2}+kx - 14$, 则 $k$ 的值为5;
(2) 已知多项式 $x^{3}-2x^{2}+ax + 2$ 能被 $x + 2$ 整除, 求 $a$ 的值.

答案： 15.解：
(1)5.
(2)$\because$多项式$x^{3}-2x^{2}+ax + 2$能被$x + 2$整除，$\therefore$当$x = - 2$时，$x^{3}-2x^{2}+ax + 2=0$，即$(-2)^{3}-2×(-2)^{2}-2a + 2=0$，解得$a = - 7$.