《2025年超越训练八年级数学上册人教版四川专版》

知识预习
物体重心的位置对于物体保持平衡、运动和稳定的状态至关重要.对于薄板、薄壳等匀质物体来说，可以将它们看成简单平面组合图形来找重心.
典例互动
例题 悬挂法确定薄板状物体的重心：如图①，用细线将薄板悬挂起来，物体静止时，在薄板上作悬线的延长线，两次悬挂所作延长线的交点 $ O $ 就是薄板的重心.如果该物体的形状是平行四边形，那么过重心 $ O $ 的任意一条直线将该物体分成面积相等的两部分.
(1)一块正方形匀质薄板按图②所示的两种方式悬挂(处于静止状态)，一块平行四边形匀质薄板按图③所示的两种方式悬挂(处于静止状态)，请用上述方法找到它们的重心 $ O $，说明重心和它们的对角线交点之间的位置关系.
(2)由两个平行四边形组合而成的平面图形如图④所示，请你结合上述材料，画一条直线平分该平面组合图形的面积.

答案：
解:
(1)如图②、图③,过悬挂点作竖直线，两条竖直线的交点即为重心$O$。观察发现，正方形和平行四边形的重心都在它们对角线的交点上。
(2)如图④，连接平行四边形的对角线，分别找到两个平行四边形的重心，连接两个平行四边形重心的直线平分该平面组合图形的面积。
　　　 　　 　

1. 小明用铅笔可以支起一张三角形薄板卡片并保持平衡，则他支起的这个点应是三角形的(C)

A.三条高的交点
B.三条角平分线的交点
C.三条中线的交点
D.无法确定

答案： 1.C

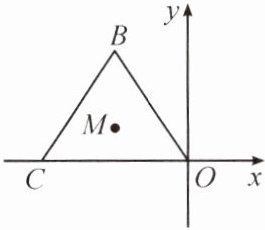
2. 三角形的重心到任意一个顶点的距离与到该顶点对边中点的距离之比为 $ 2:1 $.如图，在平面直角坐标系中，点 $ B(-2,3) $，点 $ C(-4,0) $，点 $ M $ 为 $ \triangle OBC $ 的重心.若将 $ \triangle OBC $ 绕点 $ O $ 逆时针旋转 $ 180^{\circ} $，则旋转后该三角形的重心的坐标为(2,-1).

答案： 2.(2,-1)

3. 如图，在网格平面直角坐标系中有一个四边形 $ ABCD $，$ P(1,3) $ 为该四边形的重心.请你将四边形 $ ABCD $ 分为两个三角形，使它们的重心在格点上，分别写出它们的重心坐标，并观察这两个三角形的重心位置和四边形 $ ABCD $ 的重心位置有什

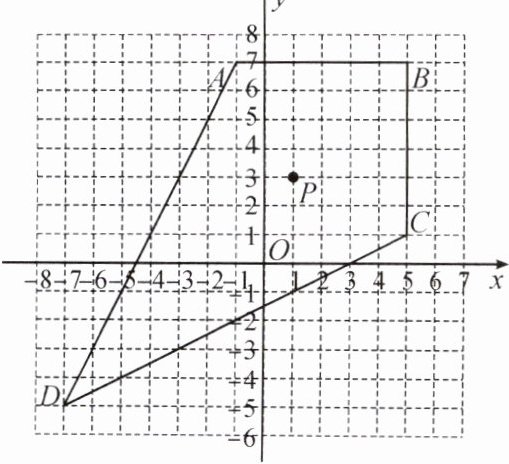
么

关系.

答案：
3.解:如图，连接$AC$，将四边形$ABCD$分成三角形$ADC$和三角形$ACB$，作图可得三角形$ADC$的重心$M$的坐标为$(-1,1)$，三角形$ACB$的重心$N$的坐标为$(3,5)$。$\because P(1,3)$，$\therefore x_{P}=\frac{1}{2}(x_{M}+x_{N}),y_{P}=\frac{1}{2}(y_{M}+y_{N})$。