第81页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
1. 下列多项式相乘的结果为 $x^2 + 3x - 18$ 的是(
A.$(x - 2)(x + 9)$
B.$(x + 2)(x - 9)$
C.$(x + 3)(x - 6)$
D.$(x - 3)(x + 6)$
D
)A.$(x - 2)(x + 9)$
B.$(x + 2)(x - 9)$
C.$(x + 3)(x - 6)$
D.$(x - 3)(x + 6)$
答案:
1.D
2. 若 $x^2 - 4x + m = (x - 2)(x + n)$,则(
A.$m = -4$,$n = 2$
B.$m = 4$,$n = -2$
C.$m = -4$,$n = -2$
D.$m = 4$,$n = 2$
B
)A.$m = -4$,$n = 2$
B.$m = 4$,$n = -2$
C.$m = -4$,$n = -2$
D.$m = 4$,$n = 2$
答案:
2.B
3. 计算 $t^2 - (t + 1)(t - 5)$ 的结果是(
A.$4t + 5$
B.$4t - 5$
C.$-4t + 5$
D.$-4t - 5$
A
)A.$4t + 5$
B.$4t - 5$
C.$-4t + 5$
D.$-4t - 5$
答案:
3.A
4. 如果 $(x + a)(x + b)$ 的展开式中不含 $x$ 的一次项,那么(
A.$ab = 1$
B.$a + b = 0$
C.$ab = 0$
D.$a + b = 1$
B
)A.$ab = 1$
B.$a + b = 0$
C.$ab = 0$
D.$a + b = 1$
答案:
4.B
5. 当 $3a - 2025 = 0$ 时,代数式 $(a - 3)(a - 4) - (a - 1)(a - 3)$ 的值为(
A.$-2017$
B.$2017$
C.$-2016$
D.$2016$
C
)A.$-2017$
B.$2017$
C.$-2016$
D.$2016$
答案:
5.C
6. 如图,长方形花园 $ABCD$ 中有两条长方形道路 $EFGH$ 和 $MNPQ$。若 $AB = a$,$AD = b$,$EF = MN = c$,则花园中可绿化部分的面积为(
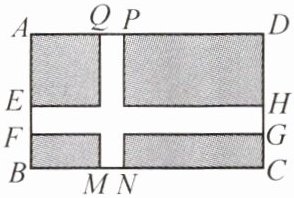
A.$bc - ab + ac + b^2$
B.$a^2 + ab + bc - ac$
C.$ab - bc - ac + c^2$
D.$b^2 - bc + a^2 - ab$
C
)
A.$bc - ab + ac + b^2$
B.$a^2 + ab + bc - ac$
C.$ab - bc - ac + c^2$
D.$b^2 - bc + a^2 - ab$
答案:
6.C
7. 如图,用若干张图①的三种卡纸拼成图②的长方形,利用面积相等可以解释的等式为 $(a + 2b)(a + b) = a^2 + 3ab + 2b^2$,则拼成图③的长方形可以解释的等式为
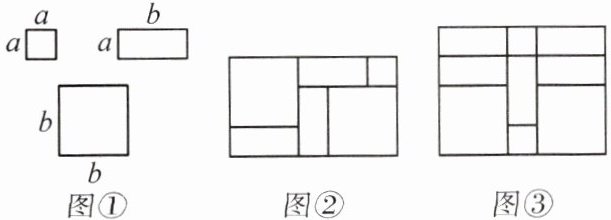
(2a+b)(a+2b)=2a²+5ab+2b²
。
答案:
7.(2a+b)(a+2b)=2a²+5ab+2b²
8. (1) 若 $a^2 + a = 1$,则 $(a - 5)(a + 6)$ 的值为
(2) 若 $a + b = 2$,$ab = -2$,则 $(2 - a)(2 - b)$ 的值为
(3) [2023·嘉兴改编] 若 $a^2 + 3ab = 5$,则 $(a + b)(a + 2b) - 2b^2$ 的值为
-29
;(2) 若 $a + b = 2$,$ab = -2$,则 $(2 - a)(2 - b)$ 的值为
-2
;(3) [2023·嘉兴改编] 若 $a^2 + 3ab = 5$,则 $(a + b)(a + 2b) - 2b^2$ 的值为
5
。
答案:
8.
(1)-29
(2)-2
(3)5
(1)-29
(2)-2
(3)5
9. 若 $(ax - b)(3x + 4) = bx^2 + cx + 72$,则 $a + b + c$ 的值为
6
。
答案:
9.6
10. 计算:
(1) [2024·重庆 B 卷节选] $a(3 - a) + (a - 1)(a + 2)$;
(2) $(x^2 - 2x + 3)(2x - 5) + 3x(3x - 2)$。
(1) [2024·重庆 B 卷节选] $a(3 - a) + (a - 1)(a + 2)$;
(2) $(x^2 - 2x + 3)(2x - 5) + 3x(3x - 2)$。
答案:
10.
(1)解:原式=4a-2。
(2)解:原式=2x³+10x-15。
(1)解:原式=4a-2。
(2)解:原式=2x³+10x-15。
11. 解不等式:$(3x + 4)(3x - 4) < 9(x - 2)(x + 3)$。
答案:
11.解:9x²-12x+12x-16<9(x²+3x-2x-6),9x²-16<9x²+9x-54,9x>38,$x>\frac{38}{9}。$
12. 先化简,再求值:$(3x - 2)(x - 3) - 2(x + 6)(x - 5) + 3(x^2 - 7x + 13)$,其中 $x = 3$。
答案:
12.解:原式=3x²-11x+6-2(x²+x-30)+3(x²-7x+13)=3x²-11x+6-2x²-2x+60+3x²-21x+39=4x²-34x+105。当x=3时,原式=39。
查看更多完整答案,请扫码查看


