《2025年超越训练八年级数学上册人教版四川专版》

13. 新定义 将 4 个数 $a$，$b$，$c$，$d$ 排成 2 行 2 列，两边各加一条竖直线，记成 $\begin{vmatrix}a&b\\c&d\end{vmatrix}$，并定义 $\begin{vmatrix}a&b\\c&d\end{vmatrix} = ad - bc$，上述记法叫作二阶行列式。根据以上信息化简求值：$\begin{vmatrix}2x&x + 2\\x - 1&x + 1\end{vmatrix}$，其中 $x$ 满足 $\frac{1}{2}x^2 + \frac{1}{2}x - 3 = 0$。

答案： 13.解：$\frac{2x}{x-1}-\frac{x+2}{x+1}=2x(x+1)-(x+2)(x-1)=2x²+2x-(x²+x-2)=2x²+2x-x²-x+2=x²+x+2。$
∵$\frac{1}{2}x²+\frac{1}{2}x-3=0，$
∴x²+x=6，
∴原式=6+2=8。

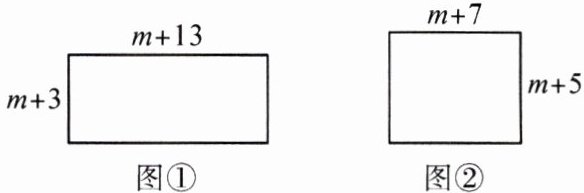
14. 如图①，长方形的两边长分别为 $m + 13$，$m + 3$，其面积记为 $S_1$；如图②，长方形的两边长分别为 $m + 7$，$m + 5$，其面积记为 $S_2$。（$m$ 为正整数）
(1) 比较 $S_1$ 与 $S_2$ 的大小。
(2) 现有一个正方形，其周长与图①中长方形的周长相等。这个正方形的面积记为 $S_3$，求 $S_3 - S_1$ 的值。

答案： 14.解：
(1)
∵S₁=(m+13)(m+3)=m²+16m+39，S₂=(m+7)(m+5)=m²+12m+35，
∴S₁-S₂=4m+4。
∵m为正整数，
∴4m+4＞0，
∴S₁＞S₂。
(2)
∵2[(m+13)+(m+3)]=4m+32=4(m+8)，
∴正方形的边长为m+8，
∴S₃=(m+8)(m+8)=m²+16m+64，
∴S₃-S₁=m²+16m+64-(m²+16m+39)=25。

15. 甲、乙两名同学计算同一道整式乘法：$(2x + a)(3x + b)$。甲抄错了第一个多项式中 $a$ 的符号，得到的结果为 $6x^2 + 11x - 10$；乙漏抄了第二个多项式中 $x$ 的系数，得到的结果为 $2x^2 - 9x + 10$。
(1) 你知道式子中 $a$，$b$ 的值各是多少吗？
(2) 请你计算这道整式乘法的正确结果。

答案： 15.解：
(1)
∵(2x-a)(3x+b)=6x²-(3a-2b)x-ab，6x²-(3a-2b)x-ab=6x²+11x-10，
∴-(3a-2b)=11。
∵(2x+a)(x+b)=2x²+(a+2b)x+ab，又2x²+(a+2b)x+ab=2x²-9x+10，
∴a+2b=-9。由$\begin{cases}-(3a-2b)=11,\\a+2b=-9,\end{cases}$得$\begin{cases}a=-5,\\b=-2.\end{cases}(2)(2x+a)(3x+b)=(2x-5)(3x-2)=6x²-19x+10。$

16. 已知代数式 $(x^2 + mx + 8)(x^2 - 3x + n)$ 的展开式中不含 $x$ 的三次项和 $x$ 的二次项。
(1) 求 $m$，$n$ 的值；
(2) 在(1)的条件下，求 $(m + n)(m^2 - mn + n^2)$ 的值。

答案： 16.解：
(1)(x²+mx+8)(x²-3x+n)=x⁴+(m-3)x³+(n-3m+8)x²+(mn-24)x+8n。由题意，得$\begin{cases}m-3=0,\\n-3m+8=0,\end{cases}$解得$\begin{cases}m=3,\\n=1.\end{cases}(2)(m+n)(m²-mn+n²)=m³-m²n+mn²+m²n-mn²+n³=m³+n³。$当m=3，n=1时，(m+n)(m²-mn+n²)=m³+n³=3³+1³=28。