《2025年超越训练八年级数学上册人教版四川专版》

A 知识预习
1. 最短路径问题的理论依据：
(1)两点之间，线段最短；(2)连接直线外一点与直线上各点的所有线段中，垂线段最短.
2. 图形的轴对称及平移的性质：
(1)连接任意一对对称点所得的线段被对称轴垂直平分；
(2)在图形的平移过程中，对应线段之间的关系是平行(或在同一条直线上)且相等.
B 典例互动

答案： 1.
(1)线段　
(2)垂线段　2.
(1)垂直平分

例 1 我们经常利用“两点之间，线段最短”来解决线段和的最值问题.
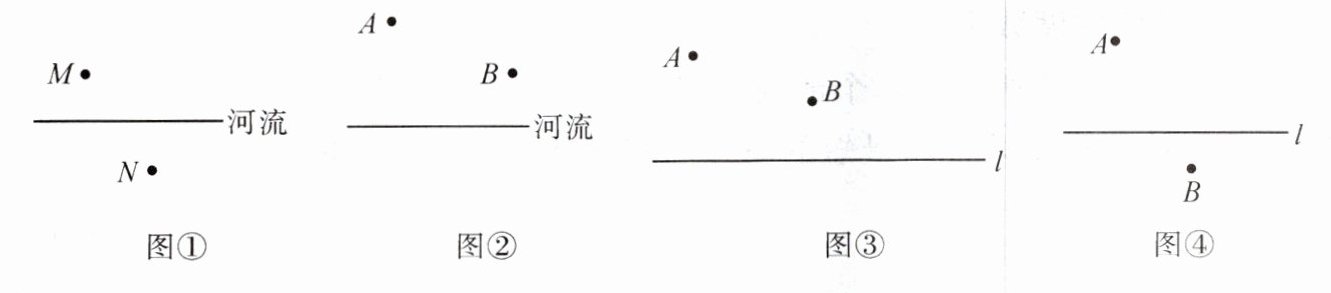
【实践运用】(1)如图①，M，N 两个小镇在河流的两侧.随着居民用水量的增加，现需要在河边修建一个自来水厂 P，分别向两个小镇供水.为了使铺设的水管最短，请在图中画出自来水厂 P 修建的位置.
(2)唐朝诗人李颀的《古从军行》中说：“白日登山望烽火，黄昏饮马傍交河”，这两句诗中隐含着一个有趣的数学问题.如图②，诗中将军在观望烽火之后从山脚下的 A 点出发，走到河边饮马后再到 B 点宿营，怎么走总路程最短？请画出最短路径.
【拓展延伸】(3)如图③，两定点 A，B 在直线 l 的同侧，在直线 l 上找一点 P，使|PA - PB|的值最大.
(4)如图④，两定点 A，B 在直线 l 的两侧，在直线 l 上找一点 P，使|PA - PB|的值最大.

答案：
例1　解:
(1)
(2)
(3)
(4)如图所示
　　　　　　 　　
　　　　　 　　

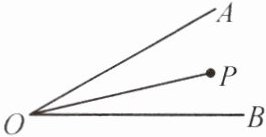
例 2 如图，∠AOB = 30°，P 为∠AOB 内的一点，OP = 10，点 M，N 分别在 OA，OB 上，求△PMN 周长的最小值.

答案：
例2　解:如图，分别作点P关于OA，OB的对称点P₁，P₂，连接P₁P₂，交OA于点M，交OB于点N，连接PM，PN，OP₁，OP₂，此时，△MPN的周长最小，最小值为P₁P₂的长.
∵OP₁ = OP = OP₂，∠P₁OP₂ = 2(∠AOP + ∠BOP) = 2∠AOB = 60°，
∴△P₁OP₂为等边三角形，
∴P₁P₂ = OP₁ = OP = 10，即△MPN周长的最小值为10.