《2025年超越训练八年级数学上册人教版四川专版》

1. 分解因式：
(1) $3ac² - 12abc =$ 3ac(c - 4b)；
(2) $a(x - a) + b(a - x) =$ (x - a)(a - b)；
(3) $9a² - 2025b² =$ 9(a + 15b)(a - 15b)；
(4) $a²(x - y) + b²(y - x) =$ (x - y)(a + b)(a - b)；
(5) $3x² + 12xy + 12y² =$ 3(x + 2y)^2；
(6) $4ab² - 4a²b - b³ =$ -b(2a - b)^2；
(7) $a² - b² - c² - 2bc =$ (a + b + c)(a - b - c)；
(8) $3x² - 8x - 3 =$ (3x + 1)(x - 3)。

答案： 1.
(1)3ac(c - 4b)
(2)(x - a)(a - b)
(3)9(a + 15b)(a - 15b)
$(4)(x - y)(a + b)(a - b) (5)3(x + 2y)^2 (6)-b(2a - b)^2$
(7)(a + b + c)(a - b - c)
(8)(3x + 1)(x - 3)

2. (1) 已知 $a - b = 5$，则 $a² - b² - 10b - 25$ 的值是 0；
(2) 如果 $4x² - 12xy + 9y² = 0$，$xy ≠ 0$，那么 $\frac{x - y}{x + y}$ 的值是 $\frac{1}{5}$；
(3) 已知 $xy = 2$，$x - 3y = 3$，则 $2x³y - 12x²y² + 18xy³ =$ 36；
(4) 若 $(x + y)² - 2x - 2y + 1 = 0$，则 $(x + y)^{2025}$ 的值是 1；
(5) 已知 $x + y = 4$，$xy = 1$，则 $(x² + 1)(y² + 1)$ 的值是 16。

答案： 2.
(1)0
(2)$\frac{1}{5}$
(3)36
(4)1
(5)16

3. 已知长方形的面积为 $4a² - 4b²$，若它的长为 $a + b$，则它的周长为 10a−6b。

答案： 3.10a−6b

4. 若 $x - 2$ 是整式 $x² + 2x + k$ 的一个因式，则 $k$ 的值是 -8。

答案： 4.-8

5. 已知 $\triangle ABC$ 的三边长 $a$，$b$，$c$ 满足 $a² + b² - 6a - 8b + 25 = 0$，$c$ 是奇数，则 $\triangle ABC$ 的周长是 10或12。

答案： 5.10或12

6. 已知 $a$，$b(a ＞ b)$ 满足 $a + b = 4$，$a² + b² = 10$，求 $a²b - ab²$ 的值。

答案： 6.解：$\because a + b = 4$，$\therefore (a + b)^2 = 16$，即$a^2 + 2ab + b^2 = 16$。又$a^2 +b^2 = 10$，$\therefore 10 + 2ab = 16$，$\therefore ab = 3$，$\therefore (a - b)^2 = (a + b)^2 - 4ab =16 - 12 = 4$。又$a ＞ b$，$\therefore a - b = 2$，$\therefore a^2b - ab^2 = ab(a - b) = 3×2 = 6$。

7. 如图，将 4 张长为 $a$，宽为 $b(a ＞ b)$ 的长方形纸片拼成一个边长为 $(a + b)$ 的正方形，图中空白部分的面积为 $S₁$，阴影部分的面积为 $S₂$。若 $S₁ = 2S₂$，试探究 $a$ 与 $b$ 之间的数量关系。

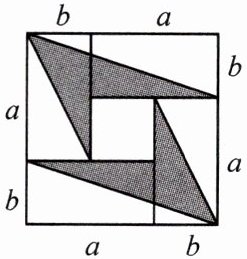
答案： 7.解：$S_1=\frac{1}{2}b(a + b)×2+\frac{1}{2}ab×2+(a - b)^2=a^2 + 2b^2$，$S_2 =(a + b)^2 - S_1=(a + b)^2 - (a^2 + 2b^2)=2ab - b^2$。$\because S_1 = 2S_2$，
$\therefore a^2 + 2b^2 = 2(2ab - b^2)$，即$a^2 - 4ab + 4b^2 = 0$，$\therefore (a - 2b)^2 = 0$，
$\therefore a - 2b = 0$，$\therefore a = 2b$。

8. 已知 $m$，$n$ 是 $\triangle ABC$ 的两条边的长，且满足 $10m² + 4n² + 4 = 12mn + 4m$。若该三角形第三边的长 $k$ 是奇数，求 $k$ 的值。

答案： 8.解：$\because 10m^2 + 4n^2 + 4 = 12mn + 4m$，$\therefore 10m^2 + 4n^2 - 12mn -4m + 4 = 0$，即$(9m^2 - 12mn + 4n^2)+(m^2 - 4m + 4)=0$，$\therefore (3m -2n)^2+(m - 2)^2 = 0$。$\because (3m - 2n)^2\geq0$，$(m - 2)^2\geq0$，
$\therefore \begin{cases}3m - 2n = 0,\\m - 2 = 0.\end{cases}$解得$\begin{cases}m = 2,\\n = 3.\end{cases}$由三角形三边关系可得$1 ＜ k ＜ 5$，
$\because k$是奇数，$\therefore k = 3$。