第95页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 设a>b,用“>”或“<”填空:a + 5 ______ b + 5.
答案:
>
3. 若a > b,则3a ______ 3b.(填“>”“<”或“=”)
答案:
>
4. 若m < n,则$\frac{3}{4}$m ______ $\frac{3}{4}$n.(填“>”或“<”)
答案:
<
5. 若x > y,则2x - 6 ______ 2y - 6.(填“>”“<”或“=”)
答案:
>
6. 已知a < b,且b < 0,则ab与b²的大小关系是________.
答案:
$ab > b^{2}$
7. 若2a < 0,则a ______ 3a.(填“>”“<”或“=”)
答案:
>
8. 选择适当的不等号填空:若a < b,则-2a ______ -2b.
答案:
>
9. 若关于x的不等式ax > 2,可化为x < $\frac{2}{a}$,则a的取值范围是________.
答案:
$a < 0$
10. 比较大小:如果a < b,那么2 - 3a ______ 2 - 3b.(填“>”“<”或“=”)
答案:
>
11. 若3a < 2a,则a - 1 ______ 0.(填“>”或“<”)
答案:
<
12. 若a > b,则下列不等式错误的是 ( )
A. a - 5 > b - 5
B. -5a < -5b
C. $\frac{a}{5}$ > $\frac{b}{5}$
D. 5 - a > 5 - b
A. a - 5 > b - 5
B. -5a < -5b
C. $\frac{a}{5}$ > $\frac{b}{5}$
D. 5 - a > 5 - b
答案:
D
13. 若a < b,则下列各式一定成立的是 ( )
A. a - 1 > b - 1
B. -3a < -3b
C. 4a > 4b
D. a + 2 < b + 2
A. a - 1 > b - 1
B. -3a < -3b
C. 4a > 4b
D. a + 2 < b + 2
答案:
D
14. 下列不等式变形正确的是 ( )
A. 由a > b,得$\frac{3}{2}$a - 3 > $\frac{3}{2}$b - 3
B. 由a > b,得-3a > -3b
C. 由a²c > b²c,得a > b
D. 由a² > b²,得a > b
A. 由a > b,得$\frac{3}{2}$a - 3 > $\frac{3}{2}$b - 3
B. 由a > b,得-3a > -3b
C. 由a²c > b²c,得a > b
D. 由a² > b²,得a > b
答案:
A
15. 实数a,b,c满足a > b,且ac > bc,它们在数轴上的对应点的位置可以是 ( )
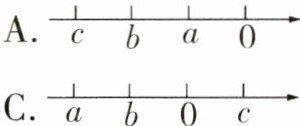
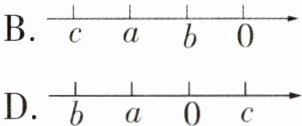
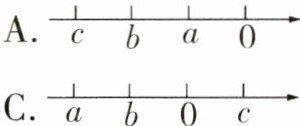

答案:
D
16. 若x < y,a < 1,则下列不等式中一定成立的是 ( )
A. ax < ay
B. x² < y²
C. x + a < y + 1
D. x - a > y - 1
A. ax < ay
B. x² < y²
C. x + a < y + 1
D. x - a > y - 1
答案:
C
17. 如图,数轴上的两点A,B对应的实数分别是a,b,则下列不等式成立的是 ( )
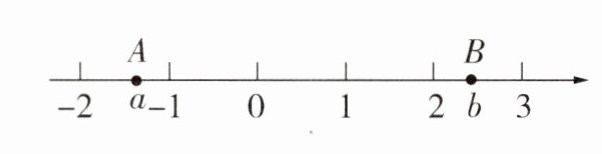
A. a < -2
B. -a < -b
C. b > 3
D. |a| < b
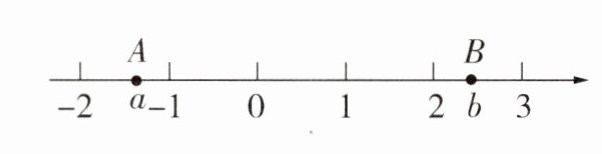
A. a < -2
B. -a < -b
C. b > 3
D. |a| < b
答案:
D
18. 若a < b < 0,则m,m - a,m - b三个数之间的大小关系是________________.(用“<”连接)
答案:
$m < m - b < m - a$
19. 已知x - y = 4.
(1)当x > 3时,y的取值范围是__________;
(2)当x > 3,y < 1时,若S = x + y,则S的取值范围是__________.
(1)当x > 3时,y的取值范围是__________;
(2)当x > 3,y < 1时,若S = x + y,则S的取值范围是__________.
答案:
(1) $y > - 1$
(2) $2 < S < 6$
(1) $y > - 1$
(2) $2 < S < 6$
20. 将下列不等式化成“x > a”或“x < a”的形式:
(1)x - 17 < -5;
(2)-\frac{1}{2}x > -3;
(3)10x - 1 > 7x.
(1)x - 17 < -5;
(2)-\frac{1}{2}x > -3;
(3)10x - 1 > 7x.
答案:
解:
(1)根据不等式的基本性质 1,两边都加 17,得 $x < 12$.
(2)根据不等式的基本性质 3,两边都乘 $-2$,得 $x < 6$.
(3)根据不等式的基本性质 1,两边都减 $7x$ 再加 1,得 $10x - 7x - 1 + 1 > 7x - 7x + 1$,即 $3x > 1$.
根据不等式的基本性质 2,两边都除以 3,得 $x > \frac{1}{3}$.
(1)根据不等式的基本性质 1,两边都加 17,得 $x < 12$.
(2)根据不等式的基本性质 3,两边都乘 $-2$,得 $x < 6$.
(3)根据不等式的基本性质 1,两边都减 $7x$ 再加 1,得 $10x - 7x - 1 + 1 > 7x - 7x + 1$,即 $3x > 1$.
根据不等式的基本性质 2,两边都除以 3,得 $x > \frac{1}{3}$.
21. 若x < y,比较2 - 3x与2 - 3y的大小,并说明理由.
答案:
解:$2 - 3x > 2 - 3y$. 理由如下:
∵ $x < y$,
∴ $-3x > - 3y$(不等式的基本性质 3),
∴ $2 - 3x > 2 - 3y$(不等式的基本性质 1).
∵ $x < y$,
∴ $-3x > - 3y$(不等式的基本性质 3),
∴ $2 - 3x > 2 - 3y$(不等式的基本性质 1).
查看更多完整答案,请扫码查看


