《2025年考出好成绩七年级数学下册鲁教版》

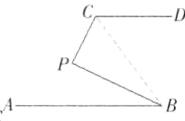
4. 如图所示，$AB// CD$.
求证：$\angle P=\angle D-\angle B$.

答案：
证明:
∵AB//CD,
∴∠AEP = ∠D.
∵∠AEP + ∠BEP = 180°,∠B + ∠P + ∠BEP = 180°,
∴∠AEP = ∠B + ∠P,
∴∠D = ∠B + ∠P,
即∠P = ∠D - ∠B.
(方法二)如图所示,过点P作PQ//AB,
∴∠B + ∠BPQ = 180°.

∵AB//CD,
∴CD//PQ,
∴∠D + ∠DPQ = 180°,
∴∠B + ∠BPQ = ∠D + ∠DPQ,
∴∠BPQ - ∠DPQ = ∠D - ∠B,
即∠BPD = ∠D - ∠B.
(方法三)如图所示,分别延长CD,PB相交于点Q.
∵AB//CD,

∴∠ABP = ∠Q.
∵∠P + ∠Q + ∠PDQ = 180°,∠PDQ + ∠CDP = 180°,
∴∠CDP = ∠P + ∠Q,
∴∠P = ∠CDP - ∠Q = ∠CDP - ∠ABP.
(方法四)如图所示,过点P作PQ//AB,
∴∠B = ∠BPQ.
∵AB//CD,

∴CD//PQ,
∴∠D = ∠DPQ.
∵∠BPD = ∠DPQ - ∠BPQ,
∴∠BPD = ∠D - ∠B.

变式4 如图所示，$\angle P=\angle D-\angle B$.
求证：$AB// CD$.

答案： 变式4:证明:
∵∠P + ∠B + ∠BEP = 180°,∠AEP + ∠BEP = 180°,
∴∠AEP = ∠B + ∠P,即∠P = ∠AEP - ∠B.
又
∵∠P = ∠D - ∠B,
∴∠AEP = ∠D,
∴AB//CD.

5. 如图所示，$AB// CD$.
求证：$\angle C+\angle P-\angle B = 180^{\circ}$.

答案：
证明:(方法一)如图所示,过点P作

PQ//AB,
∴∠B = ∠BPQ.
∵AB//CD,
∴PQ//CD,
∴∠C + ∠CPQ = 180°.
∵∠CPQ = ∠CPB - ∠BPQ,
∴∠C + ∠CPB - ∠B = 180°.
(方法二)如图所示,延长CP

交AB于点Q.
∵AB//CD,
∴∠C + ∠CQB = 180°,
∴∠CQB = 180° - ∠C.
∵∠CQB + ∠B + ∠BPQ = 180°,∠BPQ + ∠CPB = 180°,
∴∠CPB = ∠CQB + ∠B = 180° - ∠C + ∠B,
∴∠C + ∠CPB - ∠B = 180°.
(方法三)如图所示,连接CB.
∵AB//CD,
∴∠DCB =

∠CBA.
∵∠P + ∠PBC + ∠PCB = 180°,∠PBC = ∠CBA - ∠ABP,∠PCB = ∠DCP - ∠DCB,
∴∠P + ∠CBA - ∠ABP + ∠DCP - ∠DCB = 180°,
∴∠DCP + ∠P - ∠ABP = 180°.

变式5 如图所示，$\angle C+\angle P-\angle B = 180^{\circ}$.
求证：$AB// CD$.

答案：
变式5:证明:
如图所示，

过点P作PQ//AB,
∴∠B = ∠BPQ.
∵∠C + ∠P - ∠B = 180°,
∴∠C + ∠P - ∠BPQ = 180°,
即∠C + ∠CPQ = 180°,
∴CD//PQ,
∴AB//CD.

6. 如图所示，$AB// CD$，$CE$交$AB$于点$P$.
求证：$\angle B+\angle C+\angle E = 180^{\circ}$.

答案： 证明:
∵AB//CD,
∴∠C = ∠BPE.
∵∠B + ∠BPE + ∠E = 180°,
∴∠B + ∠C + ∠E = 180°.
变式6:证明:
∵∠B + ∠C + ∠E = 180°,∠B + ∠BPE + ∠E = 180°,
∴∠C = ∠BPE,
∴AB//CD.

变式6 如图所示，$\angle B+\angle C+\angle E = 180^{\circ}$.
求证：$AB// CD$.

答案： 变式6:证明:
∵∠B + ∠C + ∠E = 180°,∠B + ∠BPE + ∠E = 180°,
∴∠C = ∠BPE,
∴AB//CD.