《2025年考出好成绩七年级数学下册鲁教版》

20. 有一个小正方体，正方体的每个面分别标有1,2,3,4,5,6这六个数字. 现在有甲、乙两位同学做游戏，游戏规则是：任意掷出正方体后，如果朝上的数字是6，甲获胜；如果朝上的数字不是6，乙获胜. 你认为这个游戏规则对甲、乙双方公平吗？为什么？如果不公平，你打算怎样修改才能使游戏规则对甲、乙双方公平？

答案： 解:这个游戏不公平.理由如下:
　
∵正方体的每一个面分别标有1，2,3,4,5,6这六个数字,其中数字6 只有1个，数字不是6的有5个，
　
∴ $P(甲获胜)=\frac{1}{6}$；
　　$P(乙获胜)=\frac{5}{6}$.
　
∵ $P(甲获胜)\neq P(乙获胜)$，
　
∴此游戏不公平.
　　要使游戏公平，规则修改为:任意抛出正方体后，如果朝上的数字是奇数(1,3,5)，甲获胜；如果朝上的数字是偶数(2,4,6)，乙获胜.(答案不唯一)

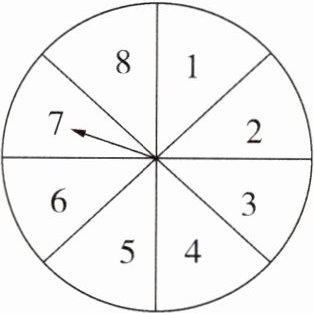
21. 今年“五一”假期期间，某超市开展有奖促销活动，凡在超市购物的顾客均有转动圆盘的机会（如图），如果规定当圆盘停下来时指针指向8就中一等奖，指向2或6就中二等奖，指向1或3或5就中三等奖，指向其余数字不中奖.
（1）转动圆盘中一等奖、二等奖、三等奖的概率分别是多少？
（2）顾客中奖的概率是多少？
（3）“五一”这天有1 800人参与这项活动，估计获得一等奖的人数是多少？

答案： 解:
(1)由题意可知,
$P(一等奖)=\frac{1}{8}$，
$P(二等奖)=\frac{1}{4}$，
$P(三等奖)=\frac{3}{8}$.
(2)转动圆盘中奖的概率为$\frac{1}{8}+\frac{1}{4}+\frac{3}{8}=\frac{6}{8}=\frac{3}{4}$
(3).获得一等奖的概率是$\frac{1}{8}$,
∴“五一”这天有1800人参与这项活动，估计获得一等奖的人数为1800x$\frac{1}{8}$=225(人).