《2025年考出好成绩七年级数学下册鲁教版》

11. 给出下列语句：①画出一个角等于两个已知角的和；②钝角总大于直角；③过点A画直线AB//CD；④相等且互补的两个角都是直角. 其中是命题的是（ ）
A. 只有④
B. ①②④
C. ②④
D. ①②③④

答案： C

12. 下列命题：①内错角相等；②无理数都是无限小数；③过一点有且只有一条直线与已知直线垂直；④过一点有且只有一条直线与已知直线平行. 其中为真命题的有（ ）
A. 0个
B. 1个
C. 2个
D. 3个

答案： B

13. 下列命题：①两直线平行，同旁内角互补；②若a = b，则a² = b²；③若两个角互补，则这两个角都是直角；④对顶角相等. 其中假命题的个数是（ ）
A. 4个
B. 3个
C. 2个
D. 1个

答案： D

14. 下列图形中，能说明“相等的角是对顶角”为假命题的是（ ）

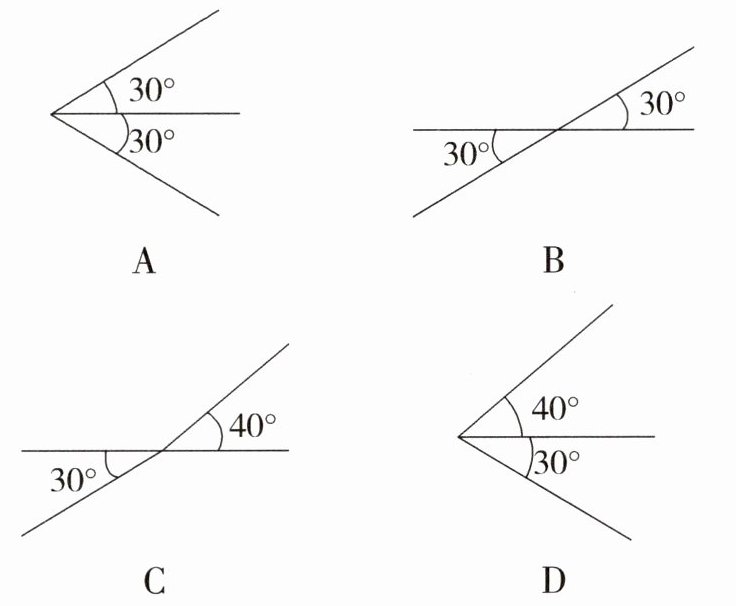
答案： A

15.（教材P38习题T2变式）如图，已知AB//CD，直线AD与直线BC有公共点，命题“内错角相等”是一个假命题，下列选项可以作为反例的是（ ）

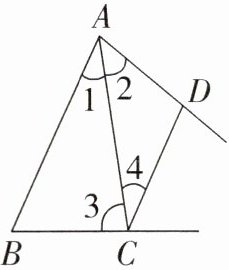
A. ∠1 = ∠4
B. ∠2 = ∠3
C. ∠1 = ∠3
D. ∠B = ∠3

答案： B

16. 把“正数的相反数是负数”改写成“如果……，那么……”的形式为如果一个数是正数，那么它的相反数是负数.

答案： 如果一个数是正数，那么它的相反数是负数

17. 把下列命题补充完整，使之成为真命题：“在同一平面内的三条直线a，b，c，若a⊥b，b//c，则a⊥c.”

答案： $a\perp c$

18. 易错点 混淆命题的条件与结论 命题：同位角相等.
（1）请将上述命题改写成“如果……，那么……”的形式，并指出这个命题的条件与结论；
（2）判断这个命题是真命题还是假命题.

答案： 解：
(1) 如果两个角是同位角，那么这两个角相等.
条件：两个角是同位角，结论：这两个角相等.
(2) 两条平行线被第三条直线所截，同位角相等，所以此命题为假命题.

19. 运算能力 阅读下面的情景对话，然后解答问题：

（1）根据“奇异三角形”的定义，小敏提出的命题“等边三角形一定是奇异三角形”是真命题；（填“真”或“假”）
（2）在Rt△ABC中，∠ACB = 90°，AB = c，AC = b，BC = a，且b ＞ a，若Rt△ABC是奇异三角形，求a : b : c的值.

答案： 解：
(1) 真.
(2) 因为在 $Rt\triangle ABC$ 中，$\angle ACB = 90^{\circ}$，$AB = c$，$AC = b$，$BC = a$，
所以根据勾股定理，得 $c^{2}=a^{2}+b^{2}$. ①
又因为 $Rt\triangle ABC$ 是奇异三角形，且 $b ＞ a$，
所以 $2b^{2}=a^{2}+c^{2}$，②
将①代入②，得 $b^{2}=2a^{2}$，即 $b = \sqrt{2}a$.
将 $b = \sqrt{2}a$ 代入①，得 $c^{2}=3a^{2}$，即 $c = \sqrt{3}a$.
则 $a:b:c = 1:\sqrt{2}:\sqrt{3}$.