第49页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 如图,已知直线a⊥c,b⊥c,∠1 = 72°,那么∠2的度数是( )
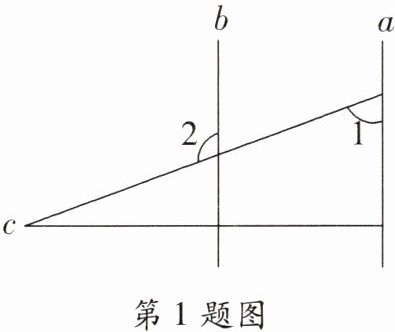
A. 72°
B. 82°
C. 92°
D. 108°

A. 72°
B. 82°
C. 92°
D. 108°
答案:
D
2. 如图,已知:AB//EF,∠B = ∠E,求证:BC//DE.
在证明该结论时,需添加辅助线,则以下关于辅助线的作法不正确的是( )
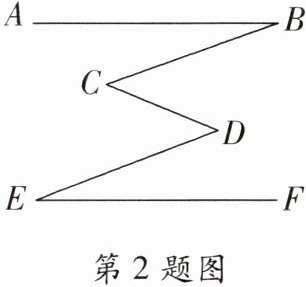
A. 延长BC交FE的延长线于点G
B. 连接BE
C. 分别作∠BCD,∠CDE的平分线CG,DH
D. 过点C作CG//AB(点G在点C左侧),过点D作DH//EF(点H在点D左侧)
在证明该结论时,需添加辅助线,则以下关于辅助线的作法不正确的是( )

A. 延长BC交FE的延长线于点G
B. 连接BE
C. 分别作∠BCD,∠CDE的平分线CG,DH
D. 过点C作CG//AB(点G在点C左侧),过点D作DH//EF(点H在点D左侧)
答案:
C
3. 如图,GA//FD,一副三角板如图摆放,∠EDF = 60°,∠BAC = 45°,若BC//DE,下列结论:①EF//AB;②∠GAB = 30°;③EC平分∠FED;④∠AED = 135°. 其中正确的个数是( )
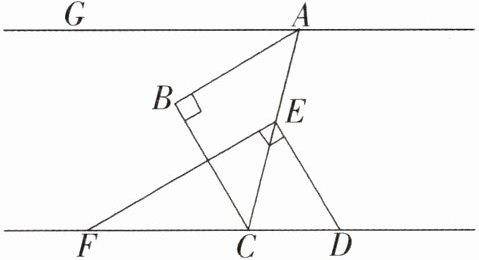
A. 1
B. 2
C. 3
D. 4

A. 1
B. 2
C. 3
D. 4
答案:
D
4. 如图,已知AB//CD,E,F,H分别为AB,CD,AC上一点(∠DFK < ∠BEK),KG平分∠EKF,∠AEK + ∠HKE = 180°,令∠BEK = α,∠DFK = β,∠GKH = γ. 则下列结论:①CD//HK;②α + β = 2∠EKG;③α - β = γ;④∠BAC + ∠AGK - ∠GKF + β = 180°. 其中正确的是__________(填序号)
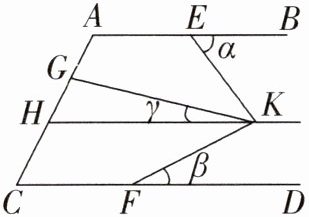

答案:
①②④
5. 已知:如图,在△ABC中,点D在BC上,连接AD,点E,F分别在AD,AB上,连接DF,且满足∠DFE = ∠C,∠1 + ∠2 = 180°.
求证:∠CAB = ∠DFB.
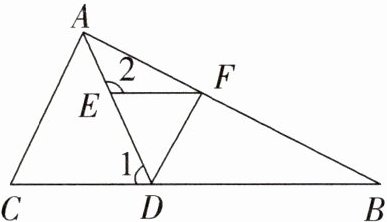
求证:∠CAB = ∠DFB.

答案:
证明:
∵$\angle 1+\angle 2 = 180^{\circ}$(已知),$\angle DEF+\angle 2 = 180^{\circ}$(邻补角的定义),
∴$\angle 1=\angle DEF$(同角的补角相等),
∴$FE// BC$(内错角相等,两直线平行),
∴$\angle DFE=\angle BDF$(两直线平行,内错角相等)。
又
∵$\angle DFE=\angle C$(已知),
∴$\angle BDF=\angle C$(等量代换),
∴$DF// AC$(同位角相等,两直线平行),
∴$\angle CAB=\angle DFB$(两直线平行,同位角相等)。
∵$\angle 1+\angle 2 = 180^{\circ}$(已知),$\angle DEF+\angle 2 = 180^{\circ}$(邻补角的定义),
∴$\angle 1=\angle DEF$(同角的补角相等),
∴$FE// BC$(内错角相等,两直线平行),
∴$\angle DFE=\angle BDF$(两直线平行,内错角相等)。
又
∵$\angle DFE=\angle C$(已知),
∴$\angle BDF=\angle C$(等量代换),
∴$DF// AC$(同位角相等,两直线平行),
∴$\angle CAB=\angle DFB$(两直线平行,同位角相等)。
查看更多完整答案,请扫码查看


