第100页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
15. 不等式$-2x + 10\geqslant0$的正整数解有( )
A. 4个
B. 5个
C. 6个
D. 7个
A. 4个
B. 5个
C. 6个
D. 7个
答案:
B
16. 新定义 定义新运算$a*b=\begin{cases}a(a < b)\\b(a\geqslant b)\end{cases}$,则不等式$(3 - 2x)*(2x + 1)<1$的解集为( )
A. $x>\frac{1}{2}$或$x<0$
B. $0<x<\frac{1}{2}$
C. $x>1$或$x<0$
D. $0<x<1$
A. $x>\frac{1}{2}$或$x<0$
B. $0<x<\frac{1}{2}$
C. $x>1$或$x<0$
D. $0<x<1$
答案:
C
17. 对于任意实数$a,b$,定义一种运算:$a※b = ab - a + b - 2$. 例如:$2※5 = 2\times5 - 2 + 5 - 2 = 11$. 请根据上述的定义解决问题:若不等式$3※x<2$,则不等式的正整数解是____.
答案:
1
18. 求不等式$\frac{0.4x - 1}{0.5}-\frac{5 - x}{2}\leqslant\frac{0.03 - 0.02x}{0.03}$的非负整数解,并把它的解集在数轴上表示出来.
答案:
解:原不等式可化为$\frac{4x - 10}{5}-\frac{5 - x}{2}\leq\frac{3 - 2x}{3}$.
去分母,得$6(4x - 10)-15(5 - x)\leq10(3 - 2x)$.
去括号,得$24x - 60 - 75 + 15x\leq30 - 20x$.
移项,得$24x + 15x + 20x\leq30 + 60 + 75$.
合并同类项,得$59x\leq165$.
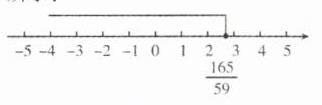
两边都除以59,得$x\leq\frac{165}{59}$.
∴原不等式的非负整数解是0,1,2.
将它的解集表示在数轴上如图所示:
解:原不等式可化为$\frac{4x - 10}{5}-\frac{5 - x}{2}\leq\frac{3 - 2x}{3}$.
去分母,得$6(4x - 10)-15(5 - x)\leq10(3 - 2x)$.
去括号,得$24x - 60 - 75 + 15x\leq30 - 20x$.
移项,得$24x + 15x + 20x\leq30 + 60 + 75$.
合并同类项,得$59x\leq165$.
两边都除以59,得$x\leq\frac{165}{59}$.
∴原不等式的非负整数解是0,1,2.
将它的解集表示在数轴上如图所示:

19. 运算能力 一个两位正整数$n$,如果$n$满足各数位上的数字互不相同且均不为0,则将$n$的两个数位上的数字对调得到一个新数$n'$. 把$n'$放在$n$的后面组成第一个四位数,把$n$放在$n'$的后面组成第二个四位数,我们把第一个四位数减去第二个四位数后再除以11所得的商记为$F(n)$,例如:$n = 23$时,$n' = 32$,$F(23)=\frac{2332 - 3223}{11}=-81$. 对于两位正整数$s$与$t$,其中$s = 10a + b$,$t = 10x + y(1\leqslant b < a\leqslant9,1\leqslant x,y\leqslant9$,且$a,b,x,y$为整数).
(1)若$F(s)$能被7整除,求$a - b$的值;
(2)在(1)的条件下,若$F(s)+81ky = kF(t)$,其中$k$为整数,求此时$s$与$t$乘积的最大值.
(1)若$F(s)$能被7整除,求$a - b$的值;
(2)在(1)的条件下,若$F(s)+81ky = kF(t)$,其中$k$为整数,求此时$s$与$t$乘积的最大值.
答案:
解:
(1) $\because s = 10a + b$,
$\therefore F(s)=\frac{(1000a + 100b + 10b + a)}{11}-\frac{(1000b + 100a + 10a + b)}{11}$
$= 81(a - b)$.
$\because F(s)$能被7整除,$1\leq b < a\leq9$,
$\therefore a - b = 7$.
(2) $\because t = 10x + y$,
$\therefore F(t)=81(x - y)$.
$\because F(s)+81ky = kF(t)$,
$\therefore 81(a - b)+81ky = k\cdot81(x - y)$.
$\because a - b = 7$,
$\therefore 81\times7 + 81ky = k\cdot81(x - y)$,
$\therefore k=\frac{7}{x - 2y}$.
$\because k$为整数,$\therefore x - 2y=\pm1$或$\pm7$.
$\because 1\leq x,y\leq9$,
$\therefore$当$x = 3$时,$y = 1$,$t = 31$;当$x = 3$时,$y = 2$,$t = 32$;
当$x = 5$时,$y = 2$,$t = 52$;当$x = 5$时,$y = 3$,$t = 53$;
当$x = 7$时,$y = 3$,$t = 73$;当$x = 7$时,$y = 4$,$t = 74$;
当$x = 9$时,$y = 4$,$t = 94$;当$x = 9$时,$y = 5$,$t = 95$;
当$x = 9$时,$y = 1$,$t = 91$;当$x = 9$时,$y = 8$,$t = 98$.
$\because a - b = 7$,$1\leq b < a\leq9$,
$\therefore a = 8$,$b = 1$或$a = 9$,$b = 2$,
$\therefore s$的值为81或92,
$\therefore st$的最大值为$92\times98 = 9016$.
(1) $\because s = 10a + b$,
$\therefore F(s)=\frac{(1000a + 100b + 10b + a)}{11}-\frac{(1000b + 100a + 10a + b)}{11}$
$= 81(a - b)$.
$\because F(s)$能被7整除,$1\leq b < a\leq9$,
$\therefore a - b = 7$.
(2) $\because t = 10x + y$,
$\therefore F(t)=81(x - y)$.
$\because F(s)+81ky = kF(t)$,
$\therefore 81(a - b)+81ky = k\cdot81(x - y)$.
$\because a - b = 7$,
$\therefore 81\times7 + 81ky = k\cdot81(x - y)$,
$\therefore k=\frac{7}{x - 2y}$.
$\because k$为整数,$\therefore x - 2y=\pm1$或$\pm7$.
$\because 1\leq x,y\leq9$,
$\therefore$当$x = 3$时,$y = 1$,$t = 31$;当$x = 3$时,$y = 2$,$t = 32$;
当$x = 5$时,$y = 2$,$t = 52$;当$x = 5$时,$y = 3$,$t = 53$;
当$x = 7$时,$y = 3$,$t = 73$;当$x = 7$时,$y = 4$,$t = 74$;
当$x = 9$时,$y = 4$,$t = 94$;当$x = 9$时,$y = 5$,$t = 95$;
当$x = 9$时,$y = 1$,$t = 91$;当$x = 9$时,$y = 8$,$t = 98$.
$\because a - b = 7$,$1\leq b < a\leq9$,
$\therefore a = 8$,$b = 1$或$a = 9$,$b = 2$,
$\therefore s$的值为81或92,
$\therefore st$的最大值为$92\times98 = 9016$.
20. 运算能力 对$m,n$定义一种新运算“$*$”,规定:$m*n = am - bn + 5(a,b$均为非零常数),等式右边的运算是通常的四则运算,例如:$3*4 = 3a - 4b + 5$. 已知$2*3 = 1$,$3*( - 1)=10$,求关于$x$的不等式$x*(2x - 3)<9$的最小整数解.
答案:
解:$\because 2*3 = 1$,$3*(-1)=10$,
$\therefore\begin{cases}2a - 3b + 5 = 1\\3a + b + 5 = 10\end{cases}$,解得$\begin{cases}a = 1\\b = 2\end{cases}$.
$\because x*(2x - 3)<9$,
$\therefore x - 2(2x - 3)+5=-3x + 11<9$,
解得$x>\frac{2}{3}$,
$\therefore$关于$x$的不等式$x*(2x - 3)<9$的最小整数解为1.
$\therefore\begin{cases}2a - 3b + 5 = 1\\3a + b + 5 = 10\end{cases}$,解得$\begin{cases}a = 1\\b = 2\end{cases}$.
$\because x*(2x - 3)<9$,
$\therefore x - 2(2x - 3)+5=-3x + 11<9$,
解得$x>\frac{2}{3}$,
$\therefore$关于$x$的不等式$x*(2x - 3)<9$的最小整数解为1.
查看更多完整答案,请扫码查看


