《2025年考出好成绩七年级数学下册鲁教版》

1. 某单位购买甲、乙两种纯净水共用250元，其中甲种水每桶8元，乙种水每桶6元；乙种水的桶数是甲种水桶数的75%。设买甲种水x桶，买乙种水y桶，则所列方程组中正确的是 （ ）
A. $\begin{cases}8x + 6y = 250,\\y = 75\%x\end{cases}$
B. $\begin{cases}8x + 6y = 250,\\x = 75\%y\end{cases}$
C. $\begin{cases}6x + 8y = 250,\\y = 75\%x\end{cases}$
D. $\begin{cases}6x + 8y = 250,\\x = 75\%y\end{cases}$

答案： A

2. 某公司用30 000元购进两种货物，货物卖出后，一种货物的利润率是10%，另一种货物的利润率是11%，共获得利润3 150元。设两种货物的进货价分别为x元，y元，根据题意列方程组为____________________。

答案： $\begin{cases}x + y = 30000, \\ 10\%x + 11\%y = 3150\end{cases}$

3. 夏季来临，天气逐渐炎热起来，某商店将某种碳酸饮料每瓶的价格上调了10%，将某种果汁饮料每瓶的价格下调了5%。已知调价前买上述碳酸饮料3瓶和果汁饮料2瓶共花费24元；调价后再买同样多的两种饮料要多花费0.6元，这两种饮料在调价前每瓶各多少元？

答案： 解:设调价前碳酸饮料每瓶$x$元，果汁饮料每瓶$y$元.
　由题意，得
　$\begin{cases}3x + 2y = 24, \\ 3(1 + 10\%)x + 2(1 - 5\%)y = 24 + 0.6\end{cases}$
解得$\begin{cases}x = 4, \\ y = 6\end{cases}$
　答:调价前碳酸饮料每瓶4元，果汁饮料每瓶6元

4. 小明家种植水果，去年收支相抵后，结余1 200元；今年因为改进了种植技术，他家水果获得丰收，收入比去年增加5%，支出比去年减少15%，今年比去年多结余1 140元。如果设小明家去年收入x元，支出为y元，那么：
（1）将有关的数据填写在下表中：

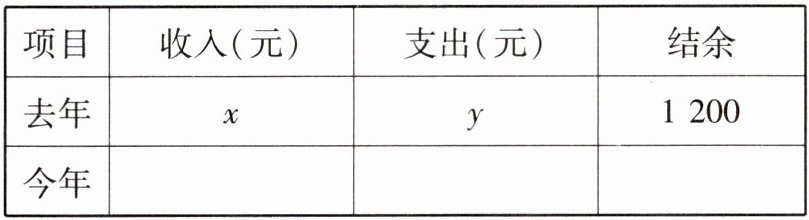
（2）根据表格列方程组____________________，解得______________。

答案：
(1)$(1 + 5\%)x$　$(1 - 15\%)y$　2340
(2)$\begin{cases}x - y = 1200, \\ 1.05x - 0.85y = 2340\end{cases}$ $\begin{cases}x = 6600, \\ y = 5400\end{cases}$

5. 某工厂去年的总产值比总支出多500万元。由于今年总产值比去年增加15%，总支出比去年节约了10%，因此，今年总产值比总支出多950万元。今年的总产值和总支出各是多少万元？
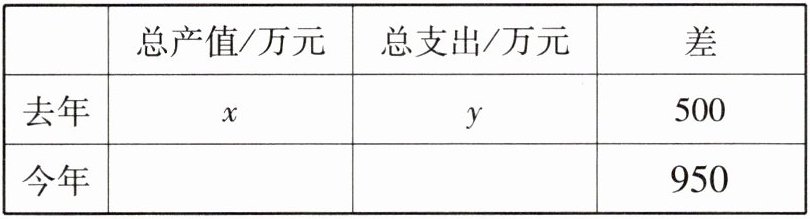
（完成下表再解答）

答案： 解:$(1 + 15\%)x$，$(1 - 10\%)y$.
　根据题意，得
　$\begin{cases}x - y = 500, \\ (1 + 15\%)x - (1 - 10\%)y = 950\end{cases}$
　解得$\begin{cases}x = 2000, \\ y = 1500\end{cases}$
　则$(1 + 15\%)x = 2300$，$(1 - 10\%)y = 1350$.
　答:今年的总产值为2300万元，总支出为1350万元

6. 甲、乙两人匀速骑车分别从相距60 km的A，B两地同时出发，若两人相向而行，则两人在出发2 h后相遇；若两人同向而行，则甲在出发6 h后追上乙。若设甲的速度为x km/h，乙的速度为y km/h，则得方程组为______________。

答案： $\begin{cases}2x + 2y = 60, \\ 6x - 6y = 60\end{cases}$

7. 易错点 忽视行程问题的数量关系 甲、乙两名同学在300米环形跑道上练习赛跑。若两人同时同地反向跑，则经过25秒两人第一次相遇；若两人同时同地同向跑，则经过150秒甲第一次追上乙。甲、乙两人的速度各是多少？

答案： 解:设甲的速度是$x$米/秒，乙的速度是$y$米/秒.
　根据题意，得
　$\begin{cases}25x + 25y = 300, \\ 150x - 150y = 300\end{cases}$
解得$\begin{cases}x = 7, \\ y = 5\end{cases}$
　答:甲的速度是7米/秒，乙的速度是5米/秒.