《2025年考出好成绩七年级数学下册鲁教版》

19. 随着通讯技术迅猛发展，人与人之间的沟通方式更多样、便捷. 为此，老师设计了“你最喜欢的沟通方式”调查问卷（每人必选且只选一种）进行调查. 将统计结果绘制了如图所示的两幅不完整的统计图，请结合图中所给的信息解答下列问题：

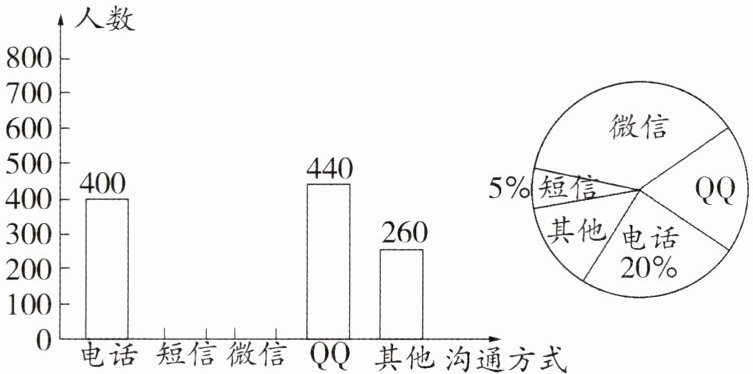
（1）这次参与调查的共有__________人；在扇形统计图中，表示“微信”的扇形圆心角的度数为______°；
（2）将条形统计图补充完整；
（3）如果我国有13亿人在使用手机.
①请估计最喜欢用“微信”进行沟通的人数；
②在全国使用手机的人中随机抽取一人，用频率估计概率，求抽取的恰好使用“QQ”的概率是多少.

答案：
解:
(1)2000,144.
　　解析:
∵最喜欢用“电话”沟通的人数为400,所占百分比为20%，
∴此次共抽查了$400\div20\% = 2000$(人)，表示“微信”的扇形圆心角的度数为$360^{\circ}\times\frac{2000 - 400 - 440 - 260 - 2000\times5\%}{2000}=144^{\circ}$.
(2)补全条形统计图如图:
　
解析:最喜欢用“短信”沟通的人数为$2000\times5\% = 100$(人)，最喜欢用“微信”沟通的人数为$2000-(400 + 440 + 260 + 100)=800$(人).
(3)①由
(2)知，参与调查的人中喜欢用“微信”进行沟通的人数有800人，
　所以在全国使用手机的13亿人中，估计最喜欢用“微信”进行沟通的人数有$13\times\frac{800}{2000}=5.2$(亿人).②由
(1)可知，参与调查的共有2000人，其中最喜欢用“QQ”进行沟通的人数为440人，
　所以在参与这次调查的人中随机抽取一人,抽取的恰好使用“QQ”的频率是$\frac{440}{2000}=0.22$，
　所以用频率估计概率，在全国使用手机的人中随机抽取一人,抽取的恰好使用“QQ”的概率是0.22.

20. 为庆祝“六一”儿童节，某玩具超市设立了一个如图所示的可以自由转动的转盘，开展有奖购买活动. 顾客购买玩具就能获得一次转动转盘的机会，当转盘停止时，指针落在哪一区域就可以获得相应奖品. 如表是该活动的一组统计数据.

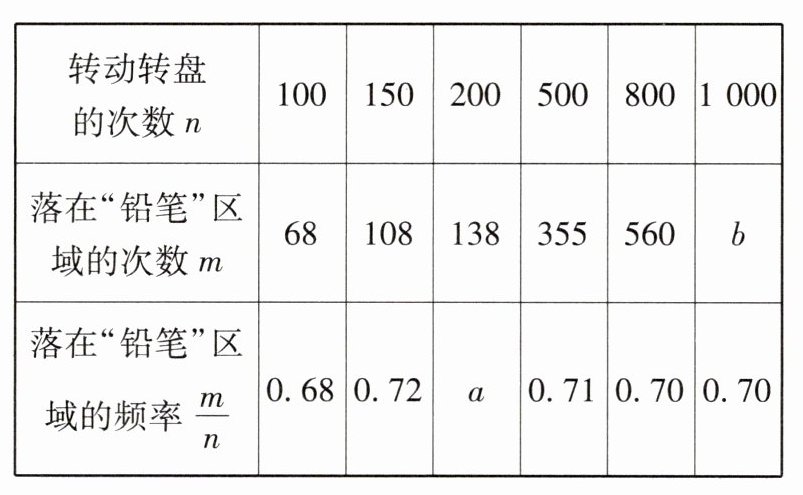
根据以上信息回答下列问题：
（1）a = _________,b = _______；
（2）试估计：假如你去转动转盘一次，获得铅笔的概率大约是_______；（结果精确到0.1）
（3）若“六一”儿童节期间共有300名顾客参与此次“转盘”活动，试估计超市大概需拿出多少个文具盒作为奖品？

答案： 解:
(1)0.69,700.
(2)0.7.
(3)
∵转动转盘一次，获得铅笔的概率大约是0.7,
∴转动转盘一次，获得文具盒的概率大约是$1 - 0.7 = 0.3$.
∵$300\times0.3 = 90$(人),
∴300名顾客参与此次“转盘”活动，估计有90人获得文具盒，
∴估计超市大概需拿出90个文具盒作为奖品.