第106页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
1. 甲、乙两车从A城出发匀速行驶至B城,在整个行驶过程中,甲、乙两车离开A城的距离y(km)与行驶时间x(h)之间的函数关系如图所示,已知甲对应的函数关系式为y = 60x,根据图象提供的信息可知,乙出发______h后超过甲车.


答案:
1.5
2. 儿童节、端午节期间,甲、乙两商场出售同种小香囊的方案如图,要使乙商场销售小香囊的营业额不低于甲商场,则乙商场至少应销售______件小香囊.


答案:
40
3. 某电商平台计划用不超过25 000元的资金购进A,B两种商品共100件,从市场得知如表信息:
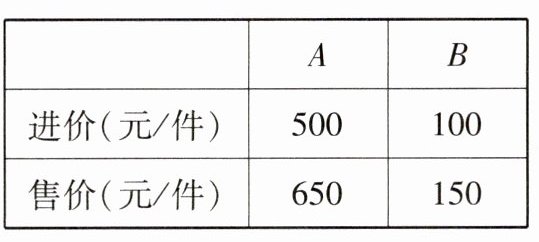
设该经销商购进A商品x件,这两种商品全部销售完后获得利润为y元.
(1)求y与x之间的函数表达式;
(2)该经销商应该如何进货可获利最大?并求出最大利润是多少元.

设该经销商购进A商品x件,这两种商品全部销售完后获得利润为y元.
(1)求y与x之间的函数表达式;
(2)该经销商应该如何进货可获利最大?并求出最大利润是多少元.
答案:
解:
(1)
∵该经销商购进A商品x件,
∴该经销商购进B商品(100 - x)件.
由题意,得y=(650 - 500)x+(150 - 100)(100 - x)=100x + 5000.
∴y与x之间的函数表达式为y = 100x + 5000.
(2)由题意,得500x + 100(100 - x)≤25000,
解得x≤37.5,且x为整数.
∵100>0,
∴y随x的增大而增大,
∴当x = 37时,y最大,
y最大=100×37 + 5000 = 8700,
∴该经销商购进A商品37件,B商品63件可获利最大,最大利润是8700元.
(1)
∵该经销商购进A商品x件,
∴该经销商购进B商品(100 - x)件.
由题意,得y=(650 - 500)x+(150 - 100)(100 - x)=100x + 5000.
∴y与x之间的函数表达式为y = 100x + 5000.
(2)由题意,得500x + 100(100 - x)≤25000,
解得x≤37.5,且x为整数.
∵100>0,
∴y随x的增大而增大,
∴当x = 37时,y最大,
y最大=100×37 + 5000 = 8700,
∴该经销商购进A商品37件,B商品63件可获利最大,最大利润是8700元.
4. 用画图象的方法解不等式2x + 1 > 3x + 4.
答案:
解:方法一:
原不等式可化为 - x - 3>0,在直角坐标系中画出函数y = - x - 3的图象(图1). 从图象可以看出,当x < - 3时这条直线上的点在x轴上方,即这时y = - x - 3>0,因此不等式的解集是x < - 3.
方法二:
把原不等式的两边看成是两个一次函数,在同一直角坐标系中画出直线y = 2x + 1与y = 3x + 4(图2). 从图象上可以看出它们的交点的横坐标是x = - 3,当x < - 3时,对于同一个x的值,直线y = 2x + 1上的点在直线y = 3x + 4上相应点的上方,此时有2x + 1>3x + 4,因此不等式的解集是x < - 3.
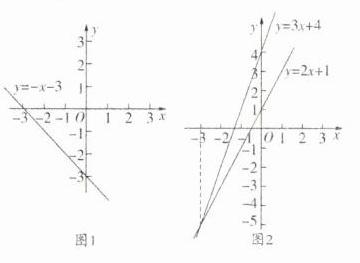
解:方法一:
原不等式可化为 - x - 3>0,在直角坐标系中画出函数y = - x - 3的图象(图1). 从图象可以看出,当x < - 3时这条直线上的点在x轴上方,即这时y = - x - 3>0,因此不等式的解集是x < - 3.
方法二:
把原不等式的两边看成是两个一次函数,在同一直角坐标系中画出直线y = 2x + 1与y = 3x + 4(图2). 从图象上可以看出它们的交点的横坐标是x = - 3,当x < - 3时,对于同一个x的值,直线y = 2x + 1上的点在直线y = 3x + 4上相应点的上方,此时有2x + 1>3x + 4,因此不等式的解集是x < - 3.

查看更多完整答案,请扫码查看


