第75页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
13. 易错点 未对c是直角边还是斜边进行分类讨论而丢解 直角三角形的三边a,b,c满足√((2 - a)²) + |b - 3| = 0,则c的值是( )
A. √5
B. √13
C. √5或√13
D. 非以上答案
A. √5
B. √13
C. √5或√13
D. 非以上答案
答案:
C
14. 如图,∠AOB = 90°,OA = 25 m,OB = 5 m,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球,如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是______m.


答案:
13
15. 已知∠ABC的两边与∠DEF的两边分别垂直,即AB⊥DE,BC⊥EF,垂足分别为点M和N,试探究:
(1) 如图1,∠B与∠E的关系是____________________;
(2) 如图2,写出∠B与∠E的关系,并说明理由;
(3) 根据上述探究,请归纳概括出一个真命题.
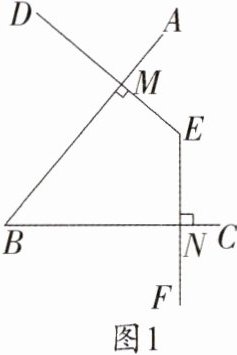

(1) 如图1,∠B与∠E的关系是____________________;
(2) 如图2,写出∠B与∠E的关系,并说明理由;
(3) 根据上述探究,请归纳概括出一个真命题.


答案:
解:
(1)$\angle B+\angle E = 180^{\circ}$.
(2)$\angle B=\angle E$.理由如下:
$\because AB\perp DE,BC\perp EF$,
$\therefore \angle BME = 90^{\circ},\angle BNE = 90^{\circ}$.
又$\because \angle BGN=\angle EGM$,
$\therefore \angle B=\angle E$.
(3)如果一个角的两边分别垂直于另一个角的两边,那么这两个角相等或互补.
(1)$\angle B+\angle E = 180^{\circ}$.
(2)$\angle B=\angle E$.理由如下:
$\because AB\perp DE,BC\perp EF$,
$\therefore \angle BME = 90^{\circ},\angle BNE = 90^{\circ}$.
又$\because \angle BGN=\angle EGM$,
$\therefore \angle B=\angle E$.
(3)如果一个角的两边分别垂直于另一个角的两边,那么这两个角相等或互补.
16. 如图,在△ABC中,AB = 6,AC = 4,点D为△ABC内一点,且∠BDC = 90°,CD = 2,BD = AC.
(1) 求BC的长;
(2) 求图中阴影部分的面积.

(1) 求BC的长;
(2) 求图中阴影部分的面积.

答案:
解:
(1)\(\because \angle BDC = 90^{\circ},CD = 2,BD=AC = 4\), \(\therefore BC=\sqrt{BD^{2}+CD^{2}}=\sqrt{4^{2}+2^{2}}=\sqrt{20}\).
(2)\(\because AB = 6,AC = 4,BC=\sqrt{20},4^{2}+(\sqrt{20})^{2}=6^{2}\),即\(AC^{2}+BC^{2}=AB^{2}\), \(\therefore \triangle ABC\)是直角三角形,\(\angle ACB = 90^{\circ}\), \(\therefore S_{阴影}=S_{\triangle ABC}-S_{\triangle BCD}=\frac{1}{2}AC\cdot BC-\frac{1}{2}CD\cdot BD=\frac{1}{2}\times4\times\sqrt{20}-\frac{1}{2}\times2\times4 = 2\sqrt{20}-4\).
(1)\(\because \angle BDC = 90^{\circ},CD = 2,BD=AC = 4\), \(\therefore BC=\sqrt{BD^{2}+CD^{2}}=\sqrt{4^{2}+2^{2}}=\sqrt{20}\).
(2)\(\because AB = 6,AC = 4,BC=\sqrt{20},4^{2}+(\sqrt{20})^{2}=6^{2}\),即\(AC^{2}+BC^{2}=AB^{2}\), \(\therefore \triangle ABC\)是直角三角形,\(\angle ACB = 90^{\circ}\), \(\therefore S_{阴影}=S_{\triangle ABC}-S_{\triangle BCD}=\frac{1}{2}AC\cdot BC-\frac{1}{2}CD\cdot BD=\frac{1}{2}\times4\times\sqrt{20}-\frac{1}{2}\times2\times4 = 2\sqrt{20}-4\).
17. 推理能力、运算能力 如图,在△ABC中,∠ACB = 90°,CE是斜边AB上的高,角平分线BD交CE于点M.
(1) 求证:△CDM是等腰三角形;
(2) 若AB = 10,AC = 8,求CM的长度.
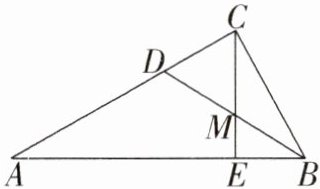
(1) 求证:△CDM是等腰三角形;
(2) 若AB = 10,AC = 8,求CM的长度.

答案:
(1)证明:\(\because BD\)平分\(\angle ABC\), \(\therefore \angle CBD=\angle ABD\). \(\because \angle ACB = 90^{\circ},CE\perp AB\), \(\therefore \angle CBD+\angle CDB = 90^{\circ},\angle ABD+\angle BME = 90^{\circ}\). \(\because \angle BME=\angle CMD\), \(\therefore \angle ABD+\angle CMD = 90^{\circ}\), \(\therefore \angle CDB=\angle CMD,
\therefore CM = CD\), \(\therefore \triangle CDM\)是等腰三角形.
(2)如图,过点\(D\)作\(DF\perp AB\)于点\(F\). \(\because \angle DCB = 90^{\circ},BD\)平分\(\angle ABC\), \(\therefore DC = DF\). \(\because \angle ACB = 90^{\circ},AB = 10,AC = 8\), \(\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-8^{2}} = 6\). \(\because S_{\triangle ABC}=S_{\triangle BCD}+S_{\triangle ADB}\), \(\therefore \frac{AC\cdot BC}{2}=\frac{BC\cdot CD}{2}+\frac{AB\cdot DF}{2}\), 即\(\frac{8\times6}{2}=\frac{6CD}{2}+\frac{10DF}{2}\), 解得\(CD = DF = 3\). 由
(1)知,\(CM = CD,
\therefore CM = 3\).
解:
(1)证明:\(\because BD\)平分\(\angle ABC\), \(\therefore \angle CBD=\angle ABD\). \(\because \angle ACB = 90^{\circ},CE\perp AB\), \(\therefore \angle CBD+\angle CDB = 90^{\circ},\angle ABD+\angle BME = 90^{\circ}\). \(\because \angle BME=\angle CMD\), \(\therefore \angle ABD+\angle CMD = 90^{\circ}\), \(\therefore \angle CDB=\angle CMD,
\therefore CM = CD\), \(\therefore \triangle CDM\)是等腰三角形.
(2)如图,过点\(D\)作\(DF\perp AB\)于点\(F\). \(\because \angle DCB = 90^{\circ},BD\)平分\(\angle ABC\), \(\therefore DC = DF\). \(\because \angle ACB = 90^{\circ},AB = 10,AC = 8\), \(\therefore BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-8^{2}} = 6\). \(\because S_{\triangle ABC}=S_{\triangle BCD}+S_{\triangle ADB}\), \(\therefore \frac{AC\cdot BC}{2}=\frac{BC\cdot CD}{2}+\frac{AB\cdot DF}{2}\), 即\(\frac{8\times6}{2}=\frac{6CD}{2}+\frac{10DF}{2}\), 解得\(CD = DF = 3\). 由
(1)知,\(CM = CD,
\therefore CM = 3\).
查看更多完整答案,请扫码查看


