《2025年考出好成绩七年级数学下册鲁教版》

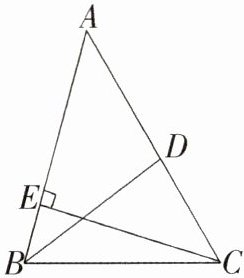
12.如图,在△ABC中,BD是∠ABC的平分线,CE 是AB边上的高,且∠ACB=60°,∠ADB=100°,求∠A和∠ACE的度数.

答案： 解:
∵∠BDC=180°−∠ADB=80°,
∴∠DBC=180°−∠BDC−∠ACB
　　=180°−80°−60°=40°.
∵BD是∠ABC的平分线，
　
∴∠ABC=80°,
∴∠A=180°−∠ABC−∠ACB =40°.
∵CE是AB边上的高，
∴∠AEC=90°,
∴∠ACE=90

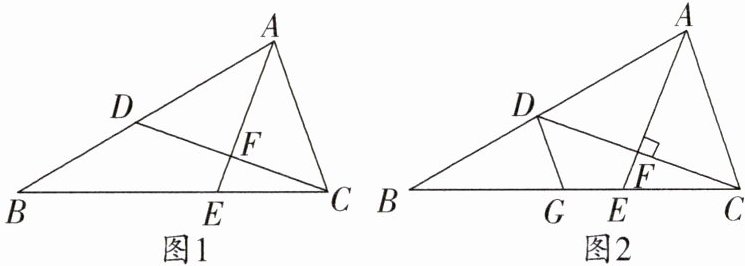
13.如图,AE是△ABC的角平分线,CD⊥AE,垂足为F,与AB交于点D.
(1)如图1,若∠BAC=80°,∠B=30°,求∠BCD的度数;
(2)如图2,点G在线段BC上,满足∠BDG=∠BAC,求证:∠GDC与∠CAE互余.

答案： 解: 解：
(1)\(\because\angle BAC = 80^{\circ},\angle B = 30^{\circ}\)， \(\therefore\angle ACB = 180^{\circ}-\angle BAC-\angle B\) \(= 70^{\circ}\)。 \(\because AE\)平分\(\angle BAC\)， \(\therefore\angle CAE=\frac{1}{2}\angle BAC = 40^{\circ}\)。 \(\because CD\perp AE,
\therefore\angle AFC = 90^{\circ}\)， \(\therefore\angle ACD = 90^{\circ}-\angle CAE = 50^{\circ}\)， \(\therefore\angle BCD=\angle ACB - \angle ACD = 20^{\circ}\)。
(2)证明：\(\because\angle BDG=\angle BAC\)， \(\therefore DG\parallel AC,
\therefore\angle GDC=\angle ACD\)。 \(\because CD\perp AE,
\therefore\angle AFC = 90^{\circ}\)， \(\therefore\angle ACD+\angle CAE = 180^{\circ}-\angle AFC\) \(= 90^{\circ}\)， \(\therefore\angle GDC+\angle CAE = 90^{\circ}\)， 即\(\angle GDC\)与\(\angle CAE\)互余。

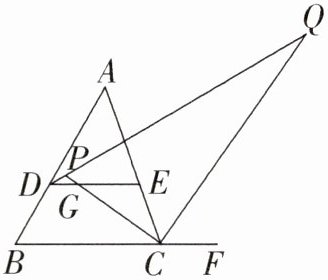
14.推理能力、运算能力　如图,在△ABC中,点D 在AB上,过点D作DE//BC,交AC于点E,DP 平分∠ADE,交∠ACB的平分线于点P,CP与DE相交于点G,∠ACF的平分线CQ与DP交于点Q.
(1)若∠A=50°,∠B=60°,则∠DPC=________，∠Q=________;
(2)若∠A=50°,当∠B的度数发生变化时，∠DPC,∠Q的度数是否发生变化？并说明理由;
(3)若△PCQ中存在一个内角等于另一个内角的三倍,请直接写出所有符合条件的∠A的度数.

答案： 解:
(1)\(115^{\circ},25^{\circ}\)。 解析：\(\because\angle A = 50^{\circ},\angle B = 60^{\circ},
\therefore\) \(\angle ACB = 70^{\circ},
\therefore\angle BCP=\frac{1}{2}\angle ACB\) \(= 35^{\circ}\)。\(\because DE\parallel BC,
\therefore\angle ADE=\angle B\) \(= 60^{\circ},\angle PGD=\angle BCP = 35^{\circ},
\therefore\) \(\angle PDE=\frac{1}{2}\angle ADE = 30^{\circ},
\therefore\angle DPC\) \(= 180^{\circ}-\angle PDE-\angle PGD = 115^{\circ}\) \(\therefore\angle CPQ = 180^{\circ}-\angle DPC = 65^{\circ}\)。又 \(\because\angle ACQ=\frac{1}{2}\angle ACF,
\therefore\angle PCQ\) \(=\angle ACQ+\angle ACP=\frac{1}{2}(\angle ACF +\) \(\angle ACB)=90^{\circ},
\therefore\angle Q = 90^{\circ}-\) \(\angle CPQ = 25^{\circ}\)。
(2)\(\angle DPC,\angle Q\)的度数不会发生变化。理由如下： \(\because DE\parallel BC\)， \(\therefore\angle ADE=\angle B\)。 \(\because DP\)平分\(\angle ADE,CP\)平分\(\angle ACB\)， \(\therefore\angle PDE=\frac{1}{2}\angle ADE=\frac{1}{2}\angle B\)， \(\angle PGD=\angle BCP=\frac{1}{2}\angle ACB\)， \(\therefore\angle DPC = 180^{\circ}-\angle PDE-\angle PGD\) \(= 180^{\circ}-\frac{1}{2}\angle B-\frac{1}{2}\angle ACB = 180^{\circ}\) \(-\frac{1}{2}(\angle B+\angle ACB)=180^{\circ}-\frac{1}{2}\) \((180^{\circ}-\angle A)=90^{\circ}+\frac{1}{2}\angle A = 115^{\circ}\)， \(\therefore\angle CPQ = 180^{\circ}-\angle DPC = 65^{\circ}\)。 又\(\because\angle PCQ=\angle ACQ+\angle ACP=\frac{1}{2}\) \((\angle ACF+\angle ACB)=90^{\circ}\)， \(\therefore\angle Q = 90^{\circ}-\angle CPQ = 25^{\circ}\)。
(3)\(\angle A = 45^{\circ}\)或\(60^{\circ}\)或\(120^{\circ}\)或\(135^{\circ}\)。 解析：设\(\angle A = x\)，则\(\angle DPC = 90^{\circ}+\) \(\frac{1}{2}x,
\therefore\angle QPC = 180^{\circ}-\angle DPC = \) \(90^{\circ}-\frac{1}{2}x\)。\(\because CP\)平分\(\angle ACB,CQ\)平 分\(\angle ACF,
\therefore\angle ACP=\frac{1}{2}\angle ACB\)， \(\angle ACQ=\frac{1}{2}\angle ACF,
\therefore\angle PCQ=\frac{1}{2}(\) \(\angle ACB+\angle ACF)=90^{\circ},\angle Q = 90^{\circ}\) \(-\angle QPC=\frac{1}{2}x\)。\(\because\triangle PCQ\)中存在 一个内角等于另一个内角的三倍， \(\therefore\)①当\(\angle Q = 3\angle QPC\)时，\(\frac{1}{2}x =\) \(3(90^{\circ}-\frac{1}{2}x),
\therefore x = 135^{\circ}\)；②当 \(\angle QPC = 3\angle Q\)时，\(90^{\circ}-\frac{1}{2}x = 3\times\) \(\frac{1}{2}x,
\therefore x = 45^{\circ}\)；③当\(\angle PCQ = 3\angle Q\) 时，\(90^{\circ}=3\times\frac{1}{2}x,
\therefore x = 60^{\circ}\)；④当 \(\angle PCQ = 3\angle QPC\)时，\(90^{\circ}=3\times(90^{\circ}\) \(-\frac{1}{2}x),
\therefore x = 120^{\circ}\)。综上所述，\(\angle A\) \(= 45^{\circ}\)或\(60^{\circ}\)或\(120^{\circ}\)或\(135^{\circ}\)。