《2025年考出好成绩七年级数学下册鲁教版》

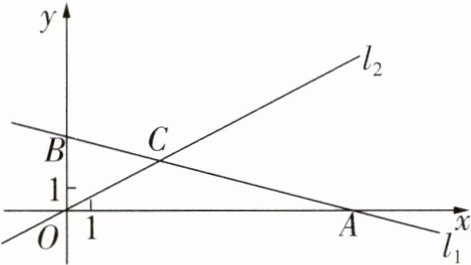
17. 如图，在直角坐标系$xOy$中，一次函数$y = kx + b$的图象$l_1$分别与$x$轴，$y$轴交于$A(15,0),B$两点，正比例函数$y = \frac{1}{2}x$的图象$l_2$与$l_1$交于点$C(m,3)$.
(1) 求$m$的值及直线$l_1$的表达式；
(2) 根据图象，直接写出不等式$kx + b ＞ \frac{1}{2}x$的解集；
(3) 求$\triangle BOC$的面积.

答案： 解:
(1)把C(m,3)代入正比例函数y=x2,得3=2m,
　解得m=6,
∴C(6,3).
∵一次函数y=kx+b的图象l1分别过A(15,0),C(6,3),
∴{615kk++bb==30,,解得{k=−$\frac{1}{3}$
　　　　　　　　　　b=5,
∴直线的表达式为y=−x1　+5.
(2)由图象可知,不等式kx+b＞$\frac{1}{2}$x 的解集是x＜6.
(3)令x=0,则y=−3x+5=5,
∴B(0,5),
∴OB=5,
∴△BOC的面积=$\frac{1}{2}$OB.xC=$\frac{1}{2}$x 5×6=15.

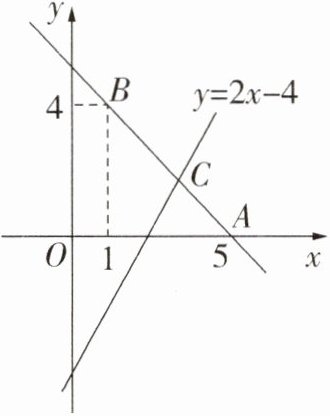
18. 已知直线$y = kx + b$经过点$B(1,4)$，且与直线$y = -x - 11$平行.
(1) 求直线$AB$的表达式并求出点$C$的坐标；
(2) 根据图象，写出关于$x$的不等式$0 ＜ 2x - 4 ＜ kx + b$的解集；
(3) 现有一点$P$在直线$AB$上，过点$P$作$PQ// y$轴交直线$y = 2x - 4$于点$Q$，若点$C$到线段$PQ$的距离为$1$，求点$P$的坐标及线段$PQ$的长.

答案： 18. 解：
(1)\(\because\)直线\(y = kx + b\)与直线\(y=-x - 11\)平行， \(\therefore k=-1\). \(\because\)直线\(y=-x + b\)经过点\(B(1,4)\)， \(\therefore -1 + b = 4\)，解得\(b = 5\)， \(\therefore\)直线\(AB\)的表达式为\(y=-x + 5\). \(\because\)直线\(y = 2x - 4\)与直线\(AB\)相交于点\(C\)， \(\therefore\begin{cases}y=-x + 5\\y = 2x - 4\end{cases}\)，解得\(\begin{cases}x = 3\\y = 2\end{cases}\)， \(\therefore\)点\(C\)的坐标为\((3,2)\).
(2)在\(y = 2x - 4\)中， 当\(y = 0\)时，\(2x - 4 = 0\)，解得\(x = 2\). 根据图象，得关于\(x\)的不等式\(0 < 2x-4 < kx + b\)的解集是\(2 < x < 3\).
(3)\(\because\)点\(C(3,2)\)到线段\(PQ\)的距离为\(1\)，\(PQ\parallel y\)轴， \(\therefore\)点\(P\)的横坐标为\(2\)或\(4\). \(\because\)点\(P\)在直线\(AB\)上， \(\therefore\)当\(x = 2\)时，\(y=-2 + 5 = 3\)；当\(x = 4\)时，\(y=-4 + 5 = 1\). \(\therefore\)点\(P\)的坐标为\((2,3)\)或\((4,1)\). \(\because PQ\parallel y\)轴交直线\(y = 2x - 4\)于点\(Q\)， \(\therefore\)当\(x = 2\)时，\(y = 2\times2 - 4 = 0\)；当\(x = 4\)时，\(y = 2\times4 - 4 = 4\). \(\therefore\)点\(Q\)的坐标为\((2,0)\)或\((4,4)\)， \(\therefore PQ = 3 - 0 = 3\)，或\(PQ = 4 - 1 = 3\). \(\therefore\)线段\(PQ\)的长为\(3\).