第93页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
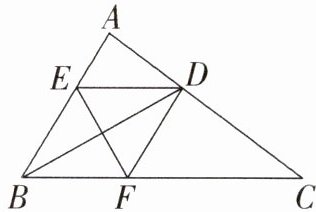
15. 如图,在△ABC中,BD是∠ABC的平分线,EF垂直平分BD. 求证:∠ABD = ∠BDF.

答案:
15. 证明:
∵ \(EF\) 垂直平分 \(BD\),
∴ \(FB = FD\),
∴ \(\angle FBD = \angle BDF\).
∵ \(BD\) 是 \(\angle ABC\) 的平分线,
∴ \(\angle ABD = \angle FBD\),
∴ \(\angle ABD = \angle BDF\).
∵ \(EF\) 垂直平分 \(BD\),
∴ \(FB = FD\),
∴ \(\angle FBD = \angle BDF\).
∵ \(BD\) 是 \(\angle ABC\) 的平分线,
∴ \(\angle ABD = \angle FBD\),
∴ \(\angle ABD = \angle BDF\).
16. 如图,在Rt△ABC中,∠ACB = 90°,∠BAC的平分线交BC于点D. 过点C作CG⊥AB于点G,交AD于点E. 过点D作DF⊥AB于点F. 下列结论:
①∠CED = ∠CDE;②∠ADF = 2∠ECD;③$S_{△AEC}:S_{△AEG} = AC:AG$;④$S_{△CED} = S_{△DFB}$;⑤CE = DF. 其中正确结论的序号是 ( )
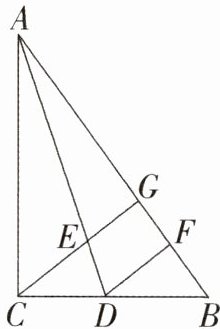
A. ①③④
B. ①②⑤
C. ③④⑤
D. ①③⑤
①∠CED = ∠CDE;②∠ADF = 2∠ECD;③$S_{△AEC}:S_{△AEG} = AC:AG$;④$S_{△CED} = S_{△DFB}$;⑤CE = DF. 其中正确结论的序号是 ( )

A. ①③④
B. ①②⑤
C. ③④⑤
D. ①③⑤
答案:
D
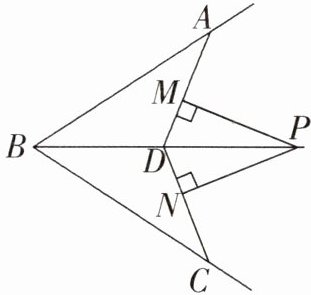
17. 如图,BD是∠ABC的平分线,AB = BC,点P在BD上,PM⊥AD,PN⊥CD,M,N分别是垂足,求证:PM = PN.

答案:
17. 证明:
∵ \(BD\) 是 \(\angle ABC\) 的平分线,
∴ \(\angle ABD = \angle CBD\). 在 \(\triangle ABD\) 和 \(\triangle CBD\) 中,
∵ \(AB = CB\),\(\angle ABD = \angle CBD\),\(BD = BD\),
∴ \(\triangle ABD\cong\triangle CBD(SAS)\),
∴ \(\angle ADB = \angle CDB\),
∴ \(\angle ADP = \angle CDP\), 即 \(DP\) 平分 \(\angle ADC\).
∵ \(PM\perp AD\),\(PN\perp CD\),
∴ \(PM = PN\).
∵ \(BD\) 是 \(\angle ABC\) 的平分线,
∴ \(\angle ABD = \angle CBD\). 在 \(\triangle ABD\) 和 \(\triangle CBD\) 中,
∵ \(AB = CB\),\(\angle ABD = \angle CBD\),\(BD = BD\),
∴ \(\triangle ABD\cong\triangle CBD(SAS)\),
∴ \(\angle ADB = \angle CDB\),
∴ \(\angle ADP = \angle CDP\), 即 \(DP\) 平分 \(\angle ADC\).
∵ \(PM\perp AD\),\(PN\perp CD\),
∴ \(PM = PN\).
18. 如图,锐角三角形ABC中,AB = AC,点D,E分别在边AB,AC上,连接BE,CD. 下列命题中,假命题是 ( )
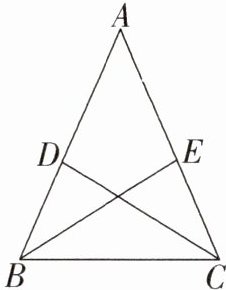
A. 若CD = BE,则∠DCB = ∠EBC
B. 若∠DCB = ∠EBC,则CD = BE
C. 若BD = CE,则∠DCB = ∠EBC
D. 若∠DCB = ∠EBC,则BD = CE

A. 若CD = BE,则∠DCB = ∠EBC
B. 若∠DCB = ∠EBC,则CD = BE
C. 若BD = CE,则∠DCB = ∠EBC
D. 若∠DCB = ∠EBC,则BD = CE
答案:
A
19. 如图,在△ABC中,∠ACB = 90°,点D为BC边上一点,E为AC延长线上的一点,CE = CD,F为CB边上一点,EF⊥射线AD于点K,过点D作直线DG⊥AB于点G,交EF于点H,作∠AGD的平分线交AD于点M,过点M作AB的平行线,交DG于点O,交BC于点Q,交EF于点N,MO = NO.
(1)找出图中和∠DHK相等的一个角,并证明;
(2)判断EH,FN,MD的数量关系,并证明.
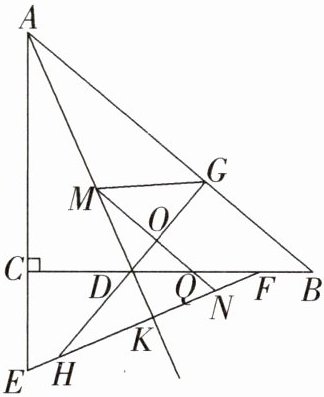
(1)找出图中和∠DHK相等的一个角,并证明;
(2)判断EH,FN,MD的数量关系,并证明.

答案:
19. 解:
(1)(答案不唯一)\(\angle DHK=\angle BAK\). 证明:如图,
∵ \(AK\perp EF\),
∴ \(\angle AKE = 90^{\circ}\),
∴ \(\angle 3 + \angle DHK = 90^{\circ}\).
∵ \(HG\perp AB\),
∴ \(\angle 2 + \angle BAK = 90^{\circ}\).
∵ \(\angle 2 = \angle 3\),
∴ \(\angle DHK = \angle BAK\).
(2) \(MD = EH + FN\). 证明:如图,连接 \(GN\).
∵ \(\angle ACB = \angle AKF = 90^{\circ}\),
∴ \(\angle 4 + \angle 5 = 90^{\circ}\),\(\angle 6 + \angle 7 = 90^{\circ}\).
∵ \(\angle 5 = \angle 6\),
∴ \(\angle 4 = \angle 7\).
∵ \(\angle ACB = \angle FCE = 90^{\circ}\),\(CD = CE\),
∴ \(\triangle ACD\cong\triangle FCE(AAS)\),
∴ \(AD = FE\).
∵ \(MN\parallel AB\),
∴ \(\angle MOD = \angle AGD = 90^{\circ}\).
∵ \(OM = ON\),
∴ \(DG\) 垂直平分 \(MN\),
∴ \(MG = NG\),\(\angle MGO = \angle HGN\).
∵ \(MG\) 平分 \(\angle AGH\),
∴ \(\angle AGM = \angle MGO\),
∴ \(\angle AGM = \angle HGN\).
∵ \(\angle MAG = \angle NHG\),\(MG = NG\),
∴ \(\triangle AMG\cong\triangle HNG(AAS)\),
∴ \(AM = HN\).
∵ \(AD = EF\),
∴ \(MD = AD - AM = EF - HN = EH + FN\).
(1)(答案不唯一)\(\angle DHK=\angle BAK\). 证明:如图,
∵ \(AK\perp EF\),
∴ \(\angle AKE = 90^{\circ}\),
∴ \(\angle 3 + \angle DHK = 90^{\circ}\).
∵ \(HG\perp AB\),
∴ \(\angle 2 + \angle BAK = 90^{\circ}\).
∵ \(\angle 2 = \angle 3\),
∴ \(\angle DHK = \angle BAK\).
(2) \(MD = EH + FN\). 证明:如图,连接 \(GN\).
∵ \(\angle ACB = \angle AKF = 90^{\circ}\),
∴ \(\angle 4 + \angle 5 = 90^{\circ}\),\(\angle 6 + \angle 7 = 90^{\circ}\).
∵ \(\angle 5 = \angle 6\),
∴ \(\angle 4 = \angle 7\).
∵ \(\angle ACB = \angle FCE = 90^{\circ}\),\(CD = CE\),
∴ \(\triangle ACD\cong\triangle FCE(AAS)\),
∴ \(AD = FE\).
∵ \(MN\parallel AB\),
∴ \(\angle MOD = \angle AGD = 90^{\circ}\).
∵ \(OM = ON\),
∴ \(DG\) 垂直平分 \(MN\),
∴ \(MG = NG\),\(\angle MGO = \angle HGN\).
∵ \(MG\) 平分 \(\angle AGH\),
∴ \(\angle AGM = \angle MGO\),
∴ \(\angle AGM = \angle HGN\).
∵ \(\angle MAG = \angle NHG\),\(MG = NG\),
∴ \(\triangle AMG\cong\triangle HNG(AAS)\),
∴ \(AM = HN\).
∵ \(AD = EF\),
∴ \(MD = AD - AM = EF - HN = EH + FN\).
查看更多完整答案,请扫码查看


