《2025年考出好成绩七年级数学下册鲁教版》

17. (教材P47习题T1变式) 已知：如图所示，∠BAF = 46°，∠ACE = 136°，CD⊥CE.
求证：CD//AB.

答案： 证明：$\because CD\perp CE,\therefore\angle DCE = 90^{\circ}$.
$\because\angle ACE = 136^{\circ}$，
$\therefore\angle ACD = 360^{\circ}-\angle ACE-\angle DCE$
$= 360^{\circ}-136^{\circ}-90^{\circ}=134^{\circ}$.
$\because\angle BAF = 46^{\circ}$，
$\therefore\angle BAC = 180^{\circ}-\angle BAF = 180^{\circ}-46^{\circ}=134^{\circ}$，
$\therefore\angle ACD=\angle BAC$，
$\therefore CD// AB$.

18. 如图所示，∠1:∠2:∠3 = 2:3:4，∠AFE = 60°，∠BDE = 120°.
求证：DE//AB，FE//BC.

答案： 证明：$\because\angle 1:\angle 2:\angle 3 = 2:3:4,\angle 1+\angle 2+\angle 3 = 180^{\circ}$，
$\therefore\angle 1 = 40^{\circ},\angle 2 = 60^{\circ},\angle 3 = 80^{\circ}$.
$\because\angle AFE = 60^{\circ},\angle BDE = 120^{\circ}$，
$\therefore\angle AFE=\angle 2,\angle BDE+\angle 2 = 180^{\circ}$，
$\therefore DE// AB,FE// BC$.

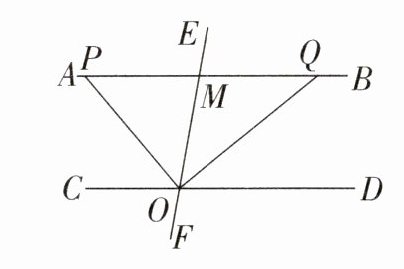
19. 推理能力 如图，直线EF与直线AB,CD分别相交于点M,O，OP,OQ分别平分∠COE和∠DOE，与AB交于点P,Q，已知∠OPQ + ∠DOQ = 90°.

(1 ) 若∠DOQ：∠DOF = 2：5，求∠FOQ的度数；
(2 ) 求证：AB//CD.

答案： 解：
(1)$\because OQ$平分$\angle DOE$，
$\therefore\angle EOQ=\angle DOQ$.
$\because\angle DOQ:\angle DOF = 2:5$，
$\therefore\angle EOQ:\angle DOQ:\angle DOF = 2:2:5$.
$\because\angle EOQ+\angle DOQ+\angle DOF = 180^{\circ}$，
$\therefore\angle EOQ=\frac{2}{2 + 2+5}\times180^{\circ}=40^{\circ}$，
$\therefore\angle FOQ = 180^{\circ}-\angle EOQ = 140^{\circ}$.
(2)证明：$\because OP,OQ$分别平分$\angle COE$和$\angle DOE$，
$\therefore\angle POM=\frac{1}{2}\angle COM,\angle QOM=\frac{1}{2}\angle DOM$，
$\therefore\angle POM+\angle QOM=\frac{1}{2}(\angle COM+\angle DOM)$，
$\therefore\angle POQ=\frac{1}{2}\angle COD=\frac{1}{2}\times180^{\circ}=90^{\circ}$，
$\therefore\angle OPQ+\angle PQO = 180^{\circ}-\angle POQ = 90^{\circ}$.
$\because\angle OPQ+\angle DOQ = 90^{\circ}$，
$\therefore\angle PQO=\angle DOQ$，
$\therefore AB// CD$.