《2025年考出好成绩七年级数学下册鲁教版》

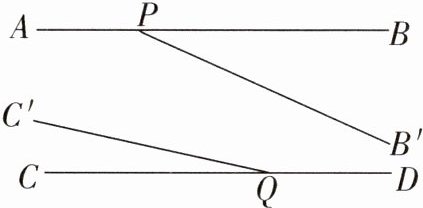
11. 易错点 忽视多种情形并存 已知直线AB//CD，点P，Q分别在AB，CD上，如图所示，射线PB按顺时针方向以每秒5°的速度旋转至PA便立即回转，并不断往返旋转；射线QC按顺时针方向每秒1°旋转至QD停止，此时射线PB也停止旋转. 若射线QC先转60秒，射线PB才开始转动，当射线PB旋转的时间为______________________秒时，PB'//QC'.

答案： 15 或 50 或 105 或 110

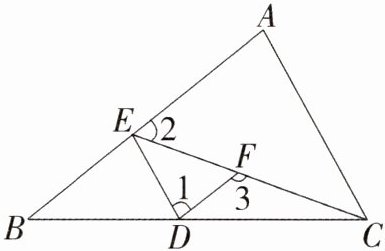
12. 如图，已知：∠A = ∠1，∠2 + ∠3 = 180°，∠BDE = 65°. 求∠ACB的度数.

答案： 解：$\because\angle2 + \angle BEC = 180^{\circ},\angle2 + \angle3 = 180^{\circ}$，
$\therefore\angle BEC = \angle3,\therefore AB// DF$，
$\therefore\angle BED = \angle1$.
$\because\angle A = \angle1,\therefore\angle BED = \angle A$，
$\therefore DE// AC$，
$\therefore\angle ACB = \angle BDE = 65^{\circ}$.

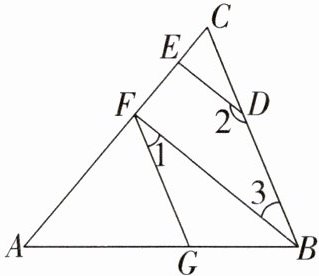
13. 如图，∠AGF = ∠ABC，∠1 + ∠2 = 180°.
（1）求证：BF//DE；
（2）若BF⊥AC，∠2 = 150°，求∠AFG的度数.

答案： 解：
(1) 证明：$\because\angle AGF = \angle ABC$，
$\therefore BC// GF,\therefore\angle1 = \angle3$.
又$\because\angle1 + \angle2 = 180^{\circ}$，
$\therefore\angle2 + \angle3 = 180^{\circ},\therefore BF// DE$.
(2) $\because\angle1 + \angle2 = 180^{\circ},\angle2 = 150^{\circ}$，
$\therefore\angle1 = 30^{\circ}$.
$\because BF\perp AC,\therefore\angle AFB = 90^{\circ}$，
$\therefore\angle AFG = \angle AFB - \angle1 = 60^{\circ}$.

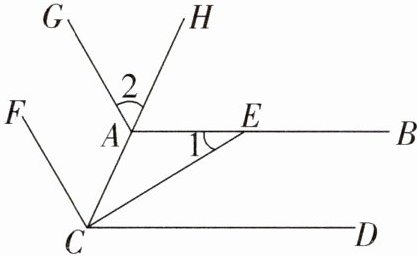
14. 如图，已知AB//CD，E是直线AB上的一点，CE平分∠ACD，射线CF⊥CE，∠1 = 32°.
（1）求∠ACE的度数；
（2）若∠2 = 58°，求证：CF//AG.

答案： 解：
(1) $\because AB// CD$，
$\therefore\angle DCE = \angle1 = 32^{\circ}$.
$\because CE$平分$\angle ACD$，
$\therefore\angle ACE = \angle DCE = 32^{\circ}$.
(2) 证明：$\because CF\perp CE$，
$\therefore\angle FCE = 90^{\circ}$，
$\therefore\angle FCH = 90^{\circ} - \angle ACE = 58^{\circ}$.
$\because\angle2 = 58^{\circ}$，
$\therefore\angle FCH = \angle2$，
$\therefore CF// AG$.

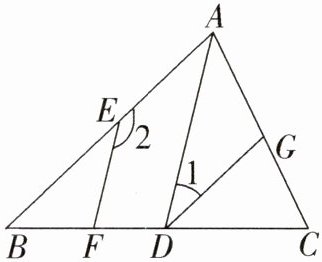
15. 如图，AB//DG，∠1 + ∠2 = 180°.
（1）求证：AD//EF；
（2）若DG是∠ADC的平分线，∠2 = 148°，求∠EFD的度数.

答案： 解：
(1) 证明：$\because AB// DG$，
$\therefore\angle BAD = \angle1$.
$\because\angle1 + \angle2 = 180^{\circ}$，
$\therefore\angle BAD + \angle2 = 180^{\circ},\therefore AD// EF$.
(2) $\because\angle2 = 148^{\circ},\angle1 + \angle2 = 180^{\circ}$，
$\therefore\angle1 = 32^{\circ}$.
$\because DG$是$\angle ADC$的平分线，
$\therefore\angle ADC = 2\angle1 = 64^{\circ}$.
$\because AD// EF$，
$\therefore\angle EFD = \angle ADC = 64^{\circ}$.