《2025年考出好成绩七年级数学下册鲁教版》

1. 请将命题“同位角相等”改写成“如果……，那么……”的形式：____________________.

答案： 如果两个角是同位角，那么这两个角相等

2. “你的作业做完了吗”这句话______命题.（填“是”或“不是”）

答案： 不是

3. 命题“同角的余角相等”的条件是____________________.

答案： 两个角是同一个角的余角

4. 下列命题是真命题的是（ ）
A. 同角的补角相等
B. 相等的角是对顶角
C. 垂直于同一条直线的两条直线平行
D. 内错角相等

答案： A

5. 有以下命题：①对顶角相等；②经过直线外一点，有且只有一条直线与已知直线平行；③同位角相等. 其中为假命题的是（ ）
A. ①②
B. ②
C. ③
D. ②③

答案： C

6. 能说明命题“若两个角α,β互补，则这两个角必为一个锐角一个钝角”是假命题的反例是____________________.

答案： $\alpha = 90^{\circ},\beta = 90^{\circ}$

7. 运算能力 观察下列算式，完成问题：
算式①：$4^{2}-2^{2}=12 = 4\times3$；
算式②：$6^{2}-4^{2}=20 = 4\times5$；
算式③：$8^{2}-6^{2}=28 = 4\times7$；
算式④：$10^{2}-8^{2}=36 = 4\times9$；
……
(1) 按照以上四个算式的规律，请写出算式⑤：____________________；
(2) 上述算式用文字表示为“任意两个连续偶数的平方差都是4的奇数倍”. 若设两个连续偶数分别为$2n$和$2n + 2$（$n$为整数），请证明上述命题成立；
(3) 命题“任意两个连续奇数的平方差都是4的奇数倍”是否成立？若成立，请证明；若不成立，请举出反例.

答案： 解：
(1)$12^{2}-10^{2}=44 = 4\times11$
(2) 证明：由题意，得$(2n + 2)^{2}-(2n)^{2}=(2n + 2 + 2n)(2n + 2 - 2n)=(4n + 2)\times2 = 4(2n + 1)$
$\because4(2n + 1)$能被4整除，且$2n + 1$为奇数
$\therefore$任意两个连续偶数的平方差都是4的奇数倍，命题成立
(3) 设两个连续奇数分别为$2n + 1$和$2n - 1$（$n$为整数）
则$(2n + 1)^{2}-(2n - 1)^{2}=(2n + 1 + 2n - 1)(2n + 1 - 2n + 1)=4n\times2 = 4\times2n$
$\because2n$是偶数
$\therefore$命题“任意两个连续奇数的平方差都是4的奇数倍”不成立
反例：$7^{2}-5^{2}=12\times2 = 24 = 4\times6$，即$7^{2}-5^{2}$是4的6倍，6是偶数，不是奇数

8. 光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射. 如图，水面$AB$与水杯下沿$CD$平行，光线$EF$从水中射向空气时发生折射，光线变成$FH$，点$C$在射线$EF$上，已知$\angle HFB = 20^{\circ}$，$\angle FED = 45^{\circ}$，则$\angle GFH$的度数为______.

答案： $25^{\circ}$

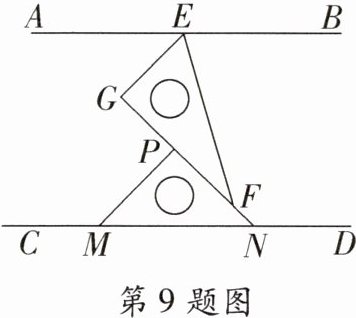
9. 如图，把一副直角三角板如图那样摆放在平行直线$AB$，$CD$之间，$\angle EFG = 30^{\circ}$，$\angle MNP = 45^{\circ}$，则：①$EG// PM$；②$\angle AEG = 45^{\circ}$；③$\angle BEF = 75^{\circ}$；④$\angle CMP = \angle EFN$. 其中正确的个数是（ ）

A. 1
B. 2
C. 3
D. 4

答案： C