《2025年考出好成绩七年级数学下册鲁教版》

10. 如图，在不添加任何字母的条件下，写出三个能判定AB//CE的条件：
①______________；
②______________；
③______________.

答案： $\angle A=\angle ECF$ $\angle B=\angle BCE$ $\angle A+\angle ACE = 180^{\circ}$

11. 如图，下列给出的条件：①∠1 = ∠3；②∠2 = ∠4；③∠DAB + ∠ABC = 180°；④∠BAD + ∠ADC = 180°. 其中可以判定AB//CD的有__________.（填序号）

答案： ①②④

12. 如图，已知∠1 = (2x + 25)°，∠2 = (4x + 35)°，要使m//n，那么x = ______.

答案： 20

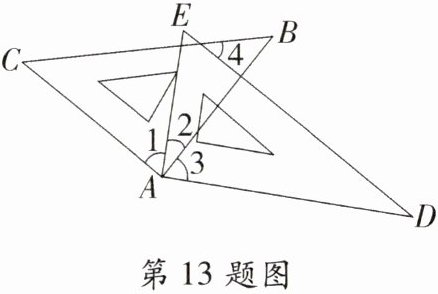
13. 易错点 忽视公共角 将一副三角板如图放置，∠BAC = ∠DAE = 90°，∠B = 45°，∠E = 60°，则下列结论：①∠1 = ∠3；②∠CAD + ∠2 = 180°；③如果∠2 = 30°，那么AC//DE；④如果∠2 = 45°，那么BC//AD. 其中正确的是___________.（填序号）

答案： ①②③④

14. 如图，给出条件：①∠C = ∠BDE；②∠C = ∠CAF；③∠B + ∠EDG = 180°；④∠BAC + ∠C = 180°. 其中能判定AB//CD的是__________.（填上所有符合条件的序号）

答案： ②③④

15. 已知：如图所示，BA交EF于点M，∠ABC = ∠E，∠E + ∠AME = 180°.
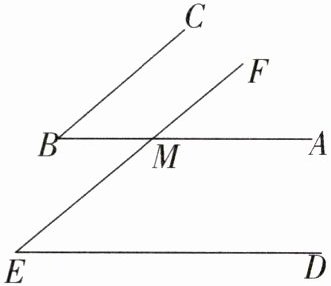
求证：BC//EF.

答案： 证明：$\because\angle ABC=\angle E,\angle E+\angle AME = 180^{\circ}$，
$\therefore\angle ABC+\angle AME = 180^{\circ}$.
$\because\angle AME=\angle BMF$，
$\therefore\angle ABC+\angle BMF = 180^{\circ}$，
$\therefore BC// EF$.

16. 已知：如图，直线EF分别与直线AB,CD相交于点P,Q，PM⊥EF，∠1 + ∠2 = 90°.
求证：AB//CD.

答案： 证明：$\because PM\perp EF$（已知），
$\therefore\angle APQ+\angle 2 = 90^{\circ}$（垂直的定义）.
$\because\angle 1+\angle 2 = 90^{\circ}$（已知），
$\therefore\angle APQ=\angle 1$（同角的余角相等），
$\therefore AB// CD$（内错角相等，两直线平行）.