《2025年考出好成绩七年级数学下册鲁教版》

12. 易错点 忽视分类讨论 在Rt△ABC中，∠BAC = 90°，有一个锐角为60°，BC = 6，点P在边BC上（不与点B，C重合），∠BAP = 30°，则CP的长为__________.

答案： 3或$\frac{9}{2}$

13. 小明想用反证法证明“如果两条直线都和第三条直线平行，那么这两条直线也互相平行”这条定理的正确性，请帮他将步骤补充完整.
已知：直线a，b，c在同一平面内，a//c，b//c.
求证：________.

答案： 解:$a// b$.
　　证明:假设$a$, $b$相交于点$A$，
　　则过点$A$有两条直线$a$, $b$都平行于$c$，
　　这与“过直线外一点有且只有一条直线与已知直线平行”相矛盾，
　　所以假设是错误的，所以$a// b$.

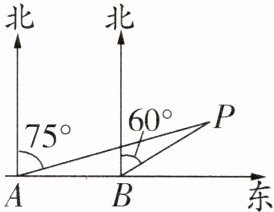
14. 已知：如图，为了躲避海盗，一轮船一直由西向东航行，早上8点，在A处测得小岛P的方向是北偏东75°，以每小时12海里的速度继续向东航行，10点到达B处，并测得小岛P的方向是北偏东60°，若小岛周围13海里内有暗礁，问该轮船是否能一直向东航行？

答案：
解:如图,过点$P$作$PD\perp AB$于点$D$.
　　　　　
　　$\because\angle PBD = 90^{\circ}-60^{\circ}=30^{\circ}$，$\angle PAB=90^{\circ}-75^{\circ}=15^{\circ}$，
　　且$\angle PBD=\angle PAB+\angle APB$，
　　$\therefore\angle PAB=\angle APB = 15^{\circ}$，
　　$\therefore BP = AB = 12\times2 = 24$（海里）.
　　在$Rt\triangle BPD$中，$\angle PBD = 30^{\circ}$，
　　$\therefore PD=\frac{1}{2}BP = 12$海里$＜13$海里，
　　$\therefore$若继续向东航行则有触礁的危险，不能一直向东航行.

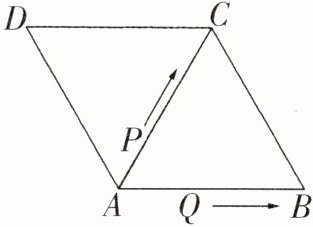
15. 推理能力 如图所示，△ABC和△ACD都是边长为4厘米的等边三角形，两个动点P，Q同时从A点出发，点P以1厘米/秒的速度沿A→C→B的方向运动，点Q以2厘米/秒的速度沿A→B→C→D的方向运动，当点Q运动到D点时，P，Q两点同时停止运动. 设P，Q运动的时间为t秒.
（1）点P，Q从出发到相遇所用时间是_____秒；
（2）当t取何值时，△APQ也是等边三角形？请说明理由；
（3）当0 ＜ t ＜ 2时，判断PQ与AC的位置关系.

答案：
解:
(1) 4.
(2)当$t=\frac{16}{3}$时，$\triangle APQ$也是等边三角形.理由如下:
　　如图1,若$\triangle APQ$是等边三角形，则此时点$P$在$BC$上，点$Q$在$CD$上.
　　易得$\triangle ADQ\cong\triangle ACP(SAS)$，
　　$\therefore CP = DQ$，即$t - 4 = 4\times3 - 2t$，
　　解得$t=\frac{16}{3}$.
　　$\therefore$当$t=\frac{16}{3}$时，$\triangle APQ$也是等边三角形.
　　
(3)如图2,取$AQ$的中点$N$，则$AQ = 2AN$.
　　根据题意，得$AQ = 2AP$，$\therefore AP = AN$.
　　又$\because\angle PAQ = 60^{\circ}$，
　　$\therefore\triangle APN$是等边三角形，
　　$\therefore PN = AN = NQ$，$\angle APN=\angle PNA = 60^{\circ}$，
　　$\therefore\angle NPQ=\angle NQP = 30^{\circ}$，
　　$\therefore\angle APQ=\angle APN+\angle NPQ = 90^{\circ}$，
　　即$PQ\perp AC$，
　　$\therefore$当$0 ＜ t ＜ 2$时，$PQ$与$AC$互相垂直.