《2025年考出好成绩七年级数学下册鲁教版》

9. 如图，在Rt△ABC中，∠ABC = 90°，ED是AC的垂直平分线，交AC于点D，交BC于点E，∠BAE = 10°，则∠C的度数是______.

答案： 40°

10. 如图所示，一辆汽车在笔直的公路AB上由A向B行驶，M，N分别是位于公路AB两侧的村庄，当汽车行驶到哪个位置时，与村庄M，N的距离相等？

答案：
解:
(1)如图,连接MN;
　
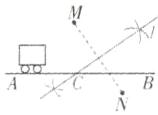
(2)作线段MN的垂直平分线l，交直线AB于点C，则当汽车行驶到点C时，与村庄M,N的距离相等

11. 如图，Rt△ABC中，∠ACB = 90°，D是AB上一点，BD = BC，过点D作AB的垂线交AC于点E，求证：BE垂直平分CD.

答案： 证明:
∵∠ACB = 90°，DE⊥AB，
　
∴∠ACB = ∠BDE = 90°.
　　在Rt△BDE和Rt△BCE中，
　
∵BD = BC，BE = BE，
　
∴Rt△BDE≌Rt△BCE(HL)，
　
∴ED = EC.
　　又
∵BD = BC，
∴BE垂直平分CD.

12. 如图，点B，E关于y轴对称，且E在AC的垂直平分线上，已知点C(5,0).
（1）如果∠BAE = 40°，那么∠C = ______；
（2）如果△ABC的周长为16 cm，AC = 6 cm，那么△ABE的周长 = ______cm；
（3）求证：AB + BO = OC.

答案： 解:
(1)35°. 解析:
∵点E在AC的垂直平分线上，
∴AE = EC，
∴∠EAC = ∠C.
∵OB = OE，AO⊥BC，
∴AB = AE，
∴∠ABE = ∠AEB = 2∠C = (180° - 40°)÷2 = 70°，
∴∠C = 35°.
(2)10. 解析:
∵△ABC的周长为16cm，AC = 6cm，
∴AB + BC = 16 - 6 = 10(cm)，
∴△ABE的周长 = AB + BE + AE = AB + BE + EC = AB + BC = 10cm.
(3)证明:
∵点B，E关于y轴对称，
∴AB = AE，OB = OE.
∵点E在AC的垂直平分线上，
∴AE = CE，
∴AB = AE = CE，
∴AB + BO = CE + OE = OC.

13. 推理能力 如图，在Rt△ABC中，∠ACB = 90°，AC = BC，D为BC边上的中点，CE⊥AD于点E，BF//AC交CE的延长线于点F，求证：AB垂直平分DF.

答案： 证明:
∵∠BCF + ∠ACE = 90°，∠ACE + ∠CAD = 90°，
　
∴∠BCF = ∠CAD.
　
∵AC⊥BC，BF//AC，
∴BF⊥BC，
　
∴∠ACD = ∠CBF = 90°.
　　又
∵AC = CB，
　
∴△ACD≌△CBF(ASA)，
　
∴CD = BF.
　
∵D为BC边上的中点，
　
∴CD = BD = $\frac{1}{2}$BC，
∴BF = BD，
∴△BFD为等腰直角三角形
∵∠ACB = 90°，CA = CB，
∴∠ABC = 45°.
∵∠FBD = 90°，
∴∠ABF = 45°，
∴∠ABC = ∠ABF，
∴BA是∠FBD的平分线，
∴AB垂直平分DF;