第97页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024云南中考)中国是最早使用正负数表示具有相反意义的量的国家.若向北运动100米记作+100米,则向南运动100米可记作( )
A.100米
B.-100米
C.200米
D.-200米
A.100米
B.-100米
C.200米
D.-200米
答案:
B
∵ 向北运动 100 米记作 +100 米,
∴ 向南运动 100 米可记作 -100 米,故选 B.
∵ 向北运动 100 米记作 +100 米,
∴ 向南运动 100 米可记作 -100 米,故选 B.
2.(2024青海中考)-2 024的相反数是( )
A.-2 024
B.2 024
C.$\frac{1}{2 024}$
D.$-\frac{1}{2 024}$
A.-2 024
B.2 024
C.$\frac{1}{2 024}$
D.$-\frac{1}{2 024}$
答案:
B -2024 的相反数是 2024,故选 B.
3.(2024山东威海中考)下列各数中,最小的数是( )
A.-2
B.-(-2)
C.$-\frac{1}{2}$
D.$-\sqrt{2}$
A.-2
B.-(-2)
C.$-\frac{1}{2}$
D.$-\sqrt{2}$
答案:
A
∵ -(-2)=2,-2< -√2< -1/2<2,
∴ -2< -√2< -1/2< -(-2),
∴ 最小的数是 -2. 故选 A.
∵ -(-2)=2,-2< -√2< -1/2<2,
∴ -2< -√2< -1/2< -(-2),
∴ 最小的数是 -2. 故选 A.
4.(2024甘肃临夏州中考)下列各数中,是无理数的是( )
A.$\frac{\pi}{2}$
B.$\frac{1}{3}$
C.$\sqrt[3]{27}$
D.0.131 33
A.$\frac{\pi}{2}$
B.$\frac{1}{3}$
C.$\sqrt[3]{27}$
D.0.131 33
答案:
A
∵ ∛27 = 3,
∴ ∛27,1/3,0.13133 是有理数,π/2 是无理数,故选 A.
∵ ∛27 = 3,
∴ ∛27,1/3,0.13133 是有理数,π/2 是无理数,故选 A.
5.(2024广东中考)完全相同的4个正方形面积之和是100,则正方形的边长是( )
A.2
B.5
C.10
D.20
A.2
B.5
C.10
D.20
答案:
B 根据题意得 √100÷4 = √25 = 5,则正方形的边长为 5. 故选 B.
6.(2024北京中考)实数a,b在数轴上的对应点的位置如图所示,下列结论中正确的是( )
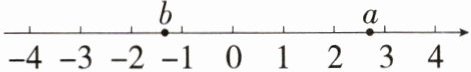
A.b>-1
B.|b|>2
C.a+b>0
D.ab>0
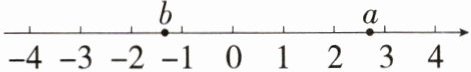
A.b>-1
B.|b|>2
C.a+b>0
D.ab>0
答案:
C 由图得,-2<b<-1,2<a<3,
∴ |b|<2,a + b>0,ab<0,故选 C.
∴ |b|<2,a + b>0,ab<0,故选 C.
7.(2024四川遂宁中考)中国某汽车公司坚持“技术为王,创新为本”的发展理念,凭借研发实力和创新的发展模式在电池、电子、乘用车、商用车和轨道交通等多个领域发挥着举足轻重的作用.2024年第一季度,该公司以62万辆的销售成绩稳居新能源汽车销量榜榜首,市场占有率高达19.4%.将销售数据用科学记数法表示为( )
A.0.62×10⁶
B.6.2×10⁶
C.6.2×10⁵
D.62×10⁵
A.0.62×10⁶
B.6.2×10⁶
C.6.2×10⁵
D.62×10⁵
答案:
C 62 万 = 620000 = 6.2×10⁵. 故选 C.
8.(2024广西中考)写出一个比$\sqrt{3}$大的整数,可以是_______.
答案:
答案 2(答案不唯一)
解析
∵ √1<√3<√4,
∴ 1<√3<2,
∴ 比 √3 大的整数可以是 2(答案不唯一).
∵ √1<√3<√4,
∴ 1<√3<2,
∴ 比 √3 大的整数可以是 2(答案不唯一).
9.(2024四川广元中考)2023年10月诺贝尔物理学奖授予三位“追光”科学家,以表彰他们“为研究物质中的电子动力学而产生阿秒光脉冲的实验方法”.什么是阿秒? 1阿秒是10⁻¹⁸秒,也就是十亿分之一秒的十亿分之一.目前世界上最短的单个阿秒光学脉冲是43阿秒,将43阿秒用科学记数法表示为_______秒.
答案:
答案 4.3×10⁻¹⁷
解析
∵ 1 阿秒是 10⁻¹⁸ 秒,
∴ 43 阿秒 = 43×10⁻¹⁸ 秒 = 4.3×10⁻¹⁷ 秒.
∵ 1 阿秒是 10⁻¹⁸ 秒,
∴ 43 阿秒 = 43×10⁻¹⁸ 秒 = 4.3×10⁻¹⁷ 秒.
10.(2024河北中考)已知a,b,n均为正整数.
(1)若n<$\sqrt{10}$<n+1,则n=_______.
(2)若n-1<$\sqrt{a}$<n,n<$\sqrt{b}$<n+1,则满足条件的a的个数总比b的个数少_______.
(1)若n<$\sqrt{10}$<n+1,则n=_______.
(2)若n-1<$\sqrt{a}$<n,n<$\sqrt{b}$<n+1,则满足条件的a的个数总比b的个数少_______.
答案:
答案 (1)3 (2)2
解析 (1)
∵ √9<√10<√16,
∴ 3<√10<4,
∵ n<√10<n + 1,n 为正整数,
∴ n = 3. (2)
∵ n - 1<√a<n,
∴ (n - 1)²<a<n²,
∴ a 的个数为 n²-(n - 1)²-1 = n² - n² + 2n - 1 - 1 = 2n - 2,
∵ n<√b<n + 1,
∴ n²<b<(n + 1)²,
∴ b 的个数为 (n + 1)² - n² - 1 = n² + 2n + 1 - n² - 1 = 2n,
∵ 2n-(2n - 2)=2,
∴ 满足条件的 a 的个数总比 b 的个数少 2.
∵ √9<√10<√16,
∴ 3<√10<4,
∵ n<√10<n + 1,n 为正整数,
∴ n = 3. (2)
∵ n - 1<√a<n,
∴ (n - 1)²<a<n²,
∴ a 的个数为 n²-(n - 1)²-1 = n² - n² + 2n - 1 - 1 = 2n - 2,
∵ n<√b<n + 1,
∴ n²<b<(n + 1)²,
∴ b 的个数为 (n + 1)² - n² - 1 = n² + 2n + 1 - n² - 1 = 2n,
∵ 2n-(2n - 2)=2,
∴ 满足条件的 a 的个数总比 b 的个数少 2.
11.(2024湖北中考)计算:(-1)×3+$\sqrt{9}$+2² - 2 024⁰.
答案:
解析 原式 = -3 + 3 + 4 - 1 = 3.
查看更多完整答案,请扫码查看


