第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
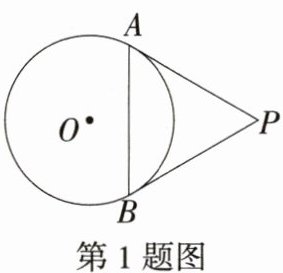
1.如图,PA,PB与⊙O分别相切于点A,B,PA = 2,∠P = 60°,则AB = (M9224010) ( )
A.$\sqrt{3}$
B.2
C.2$\sqrt{3}$
D.3

A.$\sqrt{3}$
B.2
C.2$\sqrt{3}$
D.3
答案:
B 因为PA,PB与⊙O分别相切于点A,B,所以PA = PB,又因为∠P = 60°,所以△PAB是等边三角形,所以AB = AP = 2. 故选B.
2.(2024广西南宁第十八中学月考)如图,PA,PB分别切⊙O于点A,B,连接OP交⊙O于C,下列结论不一定正确的是(M9224010) ( )

A.∠1 = ∠2
B.PA = PB
C.AB⊥OP
D.OC = PC

A.∠1 = ∠2
B.PA = PB
C.AB⊥OP
D.OC = PC
答案:
D 由切线长定理,得∠1 = ∠2,PA = PB,从而AB⊥OP,因此A、B、C中结论正确,无法得出OC = PC,D中结论不一定正确,故选D.
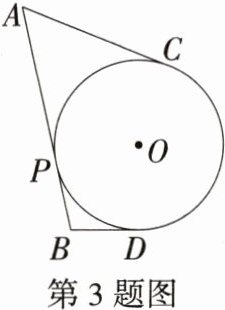
3.如图,AB,AC,BD是⊙O的切线,P,C,D为切点,若AB = 10,AC = 7,则BD的长为________.

答案:
答案 3
解析 因为AB,AC,BD是⊙O的切线,P,C,D为切点,所以AC = AP,BD = BP. 因为AB = 10,AC = 7,所以BD = BP = 10 - 7 = 3.
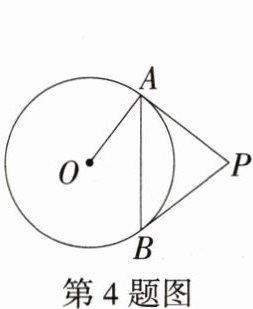
4.如图,PA,PB是⊙O的两条切线,切点分别为A,B,连接OA,AB,若∠OAB = 35°,则∠ABP = ________°. (M9224010)

答案:
答案 55
解析 因为PA,PB是⊙O的两条切线,所以PA = PB,OA⊥PA. 因为∠OAB = 35°,所以∠BAP = 90° - ∠OAB = 55°. 因为PA = PB,所以∠ABP = ∠BAP = 55°.
5.如图,已知在Rt△ABC中,∠ABC = 90°,以AB上的点O为圆心,OB的长为半径的圆与AB交于点E,与AC切于点D.求证:∠ADE = ∠ABD. (M9224010)

答案:
证明 因为∠ABC = 90°,所以OB⊥BC. 因为OB是⊙O的半径,所以CB为⊙O的切线. 又因为CD切⊙O于点D,所以BC = CD,所以∠CDB = ∠CBD. 因为BE是⊙O的直径,所以∠BDE = 90°. 所以∠ADE + ∠CDB = 90°. 因为∠ABC = 90°,所以∠ABD + ∠CBD = 90°. 所以∠ADE = ∠ABD.
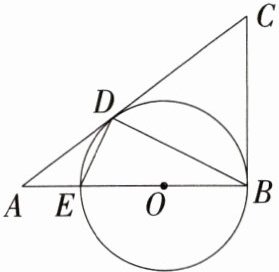
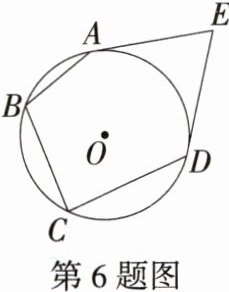
6.(2024四川泸州中考,9,★★☆)如图,EA,ED是⊙O的切线,切点为A,D,点B,C在⊙O上,若∠BAE+∠BCD = 236°,则∠E = ( )
A.56°
B.60°
C.68°
D.70°

A.56°
B.60°
C.68°
D.70°
答案:
C 连接AD,如图. 因为四边形ABCD内接于⊙O,所以∠BCD + ∠BAD = 180°. 又因为∠BAE + ∠BCD = 236°,所以∠DAE = 236° - 180° = 56°. 因为EA,ED是⊙O的切线,所以AE = DE,所以∠EDA = ∠EAD = 56°,所以∠E = 180° - 2×56° = 68°,故选C.

C 连接AD,如图. 因为四边形ABCD内接于⊙O,所以∠BCD + ∠BAD = 180°. 又因为∠BAE + ∠BCD = 236°,所以∠DAE = 236° - 180° = 56°. 因为EA,ED是⊙O的切线,所以AE = DE,所以∠EDA = ∠EAD = 56°,所以∠E = 180° - 2×56° = 68°,故选C.

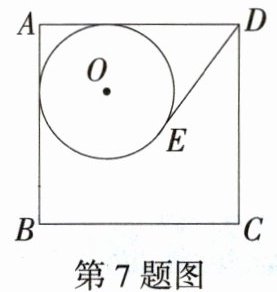
7.(2024广东广州广雅中学二模,14,★★☆)如图,圆O与正方形ABCD的两边AB,AD相切,且DE与圆O相切于E点.若圆O的半径为2,且AB = 6,则DE的长度为________.

答案:
答案 4 解析 如图,设⊙O与正方形ABCD的边AD,AB切于点F,H,连接OH,OF,OE,则∠OFD = ∠OFA = ∠OHA = 90°. 因为四边形ABCD是正方形,所以∠A = 90°,AD = AB = 6,又因为OH = OF,所以四边形AHOF是正方形. 因为⊙O的半径为2,所以OF = AF = OH = 2,所以DF = AD - AF = 6 - 2 = 4. 因为DE与⊙O相切于点E,所以DE = DF = 4.
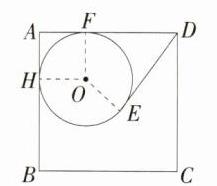
答案 4 解析 如图,设⊙O与正方形ABCD的边AD,AB切于点F,H,连接OH,OF,OE,则∠OFD = ∠OFA = ∠OHA = 90°. 因为四边形ABCD是正方形,所以∠A = 90°,AD = AB = 6,又因为OH = OF,所以四边形AHOF是正方形. 因为⊙O的半径为2,所以OF = AF = OH = 2,所以DF = AD - AF = 6 - 2 = 4. 因为DE与⊙O相切于点E,所以DE = DF = 4.

8.(2023河北冀州中学模拟,23,★★☆)图1是一种简易三分角器的示意图,其中AB与半圆O的直径BC在同一直线上,且AB的长度与半圆的半径相等,DB与AC垂直,垂足为点B,DB足够长.使用方法如图2所示,若要把∠MEN三等分,只需适当放置三分角器,使DB经过∠MEN的顶点E,点A落在边EM上,半圆O与另一边EN恰好相切,切点为F,则EB,EO就把∠MEN三等分了.
(1)请根据题意写出已知和求证.
(2)请证明这一方法的正确性.
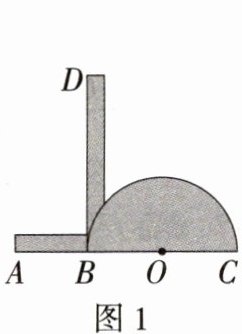
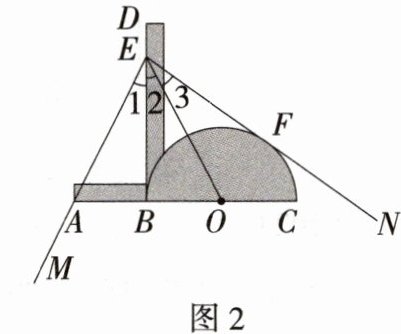
(1)请根据题意写出已知和求证.
(2)请证明这一方法的正确性.


答案:
解析 (1)已知:在题图2中,点A,B,O,C在同一直线上,AB = OB = OC,EB⊥AC,垂足为点B,半圆O与EN相切于点F,点A在射线EM上.
求证:∠1 = ∠2 = ∠3.
(2)证明:因为EB⊥AC,所以∠ABE = ∠OBE = 90°. 又因为AB = OB,BE = BE,所以△ABE≌△OBE(SAS). 所以∠1 = ∠2. 因为BE⊥OB,OB为半圆O的半径,所以BE是半圆O的切线. 因为EN切半圆O于F,所以∠2 = ∠3,所以∠1 = ∠2 = ∠3.
查看更多完整答案,请扫码查看


