《2025年5年中考3年模拟九年级数学下册沪科版》

9. 教材变式·P75T3（2024广东信宜期末）试确定图中路灯的位置，并画出此时小明在路灯下的影子.

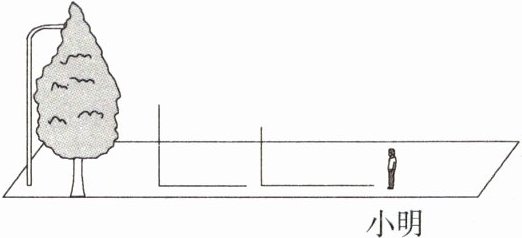
答案：
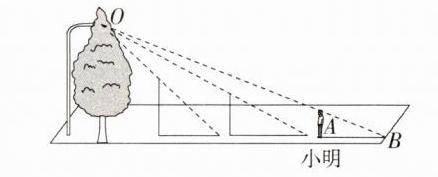
解析：如图所示，点O是路灯所在的位置，AB是小明的影子。

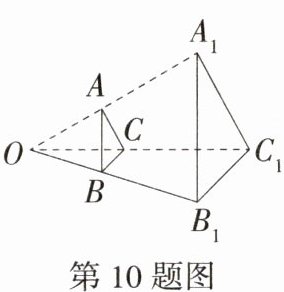
10.（2024四川凉山州中考，11，★★☆）如图，一块面积为60 cm²的三角形硬纸板（记为△ABC）平行于投影面时，在点光源O的照射下形成的投影是△A₁B₁C₁，若OB∶BB₁ = 2∶3，则△A₁B₁C₁的面积是(M9225001) （ ）

A. 90 cm²
B. 135 cm²
C. 150 cm²
D. 375 cm²

答案： D：由题意知△ABC∽△A₁B₁C₁，OB : BB₁ = 2 : 3，
∴$\frac{OB}{OB₁}=\frac{2}{5}$，
∴$\frac{S_{\triangle ABC}}{S_{\triangle A₁B₁C₁}} = (\frac{2}{5})^2=\frac{4}{25}$，
∵三角形硬纸板的面积为60 cm²，
∴△A₁B₁C₁的面积为375 cm²。故选D。

11.（2024广西桂林中学模拟，18，★★☆）某学校旁有一根电线杆AB和垂直于地面放置的一块长方形广告牌HCDF，有一天小明发现在太阳光照射下，电线杆顶端A的影子刚好落在长方形广告牌的边HF的中点G处，而长方形广告牌的点F的影子刚好落在地面上E点，如图，已知A、B、C、D、E、F、G、H均在同一平面内，BC = 5米，HF = 4米，HC = 3米，DE = 4米，则电线杆AB的高度是______米.(M9225001)

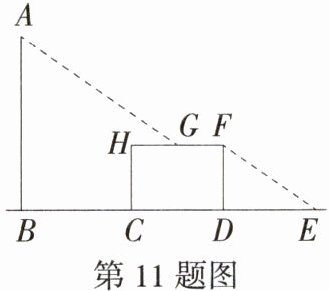
答案：
答案：$\frac{33}{4}$ 解析：如图，过点G作GQ⊥BE于点Q，GP⊥AB于点P，根据题意可得，BP = GQ = HC = DF = 3米，根据太阳光下，物体实际高度和影长成正比例，得$\frac{AP}{DF}=\frac{PG}{DE}$，
∴$\frac{AP}{3}=\frac{5 + 2}{4}$，
∴AP=$\frac{21}{4}$，
∴AB=$\frac{21}{4}+3=\frac{33}{4}$（米）。

12.（2022浙江温州中考，16，★★☆）某风车示意图如图，其相同的四个叶片均匀分布，水平地面上的点M在旋转中心O的正下方. 某一时刻，太阳光线恰好垂直照射叶片OA，OB，此时各叶片影子在点M右侧成线段CD，测得MC = 8.5 m，CD = 13 m，垂直于地面的木棒EF与影子FG的比为2∶3，则点O，M之间的距离等于_______米. 转动时，叶片外端离地面的最大高度等于_______米.

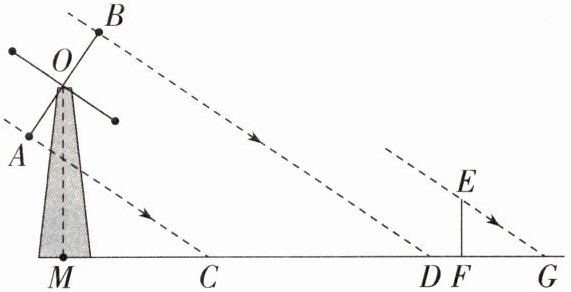
答案：
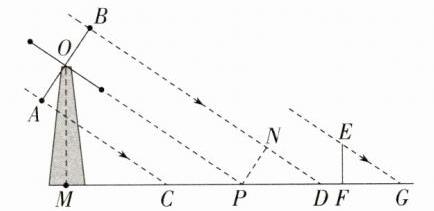
答案：10；(10 + $\sqrt{13}$) 解析：如图，过点O作OP//BD交MG于P，过P作PN⊥BD于N，则OB = PN，
∵AC//BD，
∴AC//OP//BD，
∴$\frac{OA}{OB}=\frac{CP}{PD}$，
∵OA = OB，
∴CP = PD=$\frac{1}{2}$CD = 6.5，
∴MP = MC + CP = 8.5 + 6.5 = 15，易知∠EGF = ∠OPM，
∴tan∠EGF = tan∠OPM，
∴$\frac{EF}{FG}=\frac{OM}{MP}=\frac{2}{3}$，
∴OM=$\frac{2}{3}$×15 = 10。
∵DB//EG，
∴∠EGF = ∠NDP，
∴sin∠EGF = sin∠NDP，
∴$\frac{EF}{EG}=\frac{PN}{PD}$，即$\frac{2}{\sqrt{2^2 + 3^2}}=\frac{PN}{6.5}$，
∴OB = PN=$\sqrt{13}$，易知当OB与OM共线时，叶片外端离地面的高度最大，其最大高度等于(10 + $\sqrt{13}$)米。

13.（2024山东枣庄期中，19，★★☆）如图，在平面直角坐标系中，P(4,3)是一个点光源，CD为木杆AB在P的照射下，在x轴上形成的投影，若A(0,1)，B(6,1)，过点P作PM⊥x轴，垂足为点M，PM交AB于点N，求CD的长.

答案： 解析：
∵A(0,1)，B(6,1)，
∴AB//x轴，AB = 6，
∴△PAB∽△PCD，
∴$\frac{AB}{CD}=\frac{PN}{PM}$， 易知PM = 3，PN = 2，
∴$\frac{6}{CD}=\frac{2}{3}$，
∴CD = 9，即CD的长为9。

14.（2022陕西中考，21，★★☆）小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高. 如图所示，在某一时刻，他们在阳光下，分别测得该建筑物OB的影长OC为16米，OA的影长OD为20米，小明的影长FG为2.4米，其中O、C、D、F、G五点在同一直线上，A、B、O三点在同一直线上，且AO⊥OD，EF⊥FG. 已知小明的身高EF为1.8米，求旗杆的高AB.

答案： 解析：
∵AD//EG，
∴∠ADO = ∠EGF。 又
∵∠AOD = ∠EFG = 90°，
∴△AOD∽△EFG。
∴$\frac{AO}{EF}=\frac{OD}{FG}$，
∴AO=$\frac{EF·OD}{FG}=\frac{1.8×20}{2.4}=15$。 同理可得BO = 12。
∴AB = AO - BO = 15 - 12 = 3（米）。
∴旗杆的高AB为3米。