第18页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
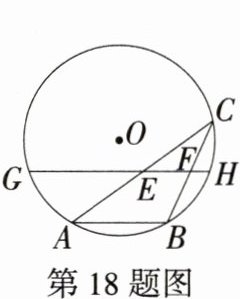
18.(2024广西河池宜州期末,18,★★☆)如图,AB是⊙O的一条弦,点C是⊙O上一动点,且∠ACB = 30°,点E、F分别是AC、BC的中点,直线EF与⊙O交于G、H两点,若⊙O的半径为8,则GE + FH的最大值为_______.

答案:
答案:12
解析:连接OA、OB(图略),因为$\angle ACB = 30^{\circ}$,所以$\angle AOB = 2\angle ACB = 60^{\circ}$。因为$OA = OB$,所以$\triangle AOB$为等边三角形。因为$\odot O$的半径为8,所以$AB = OA = OB = 8$。
因为点E,F分别是AC、BC的中点,所以$EF=\frac{1}{2}AB = 4$,要求$GE + FH$的最大值,即求$GE + FH+EF$(弦GH)的最大值,当弦GH是圆的直径时,它的值最大,最大值为$8\times2 = 16$,所以$GE + FH$的最大值为$16 - 4 = 12$。
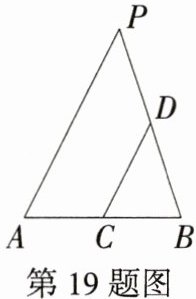
19.定边定角型问题 (2023河南郑州郑东新区春华学校期末,14,★★☆)如图,已知线段AB = 4,动点P满足∠APB = 45°,C、D分别是线段AB、BP的中点,则线段CD长度的最大值为_______.

答案:
答案:$2\sqrt{2}$ 解析:因为C、D分别是线段AB、BP的中点,所以$CD=\frac{1}{2}AP$,所以当AP长度最大时,CD的长度最大。因为线段$AB = 4$,动点P满足$\angle APB = 45^{\circ}$,所以点P在以AB为弦,圆周角$\angle APB = 45^{\circ}$的圆上运动(如图),当$AP'$为圆的直径时,$AP'$长度最大,此时$\angle ABP' = 90^{\circ}$,所以$AP'=\sqrt{2}AB = 4\sqrt{2}$,所以线段CD长度的最大值为$2\sqrt{2}$。
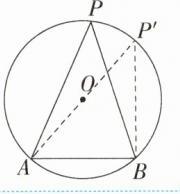
答案:$2\sqrt{2}$ 解析:因为C、D分别是线段AB、BP的中点,所以$CD=\frac{1}{2}AP$,所以当AP长度最大时,CD的长度最大。因为线段$AB = 4$,动点P满足$\angle APB = 45^{\circ}$,所以点P在以AB为弦,圆周角$\angle APB = 45^{\circ}$的圆上运动(如图),当$AP'$为圆的直径时,$AP'$长度最大,此时$\angle ABP' = 90^{\circ}$,所以$AP'=\sqrt{2}AB = 4\sqrt{2}$,所以线段CD长度的最大值为$2\sqrt{2}$。

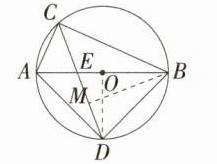
20.(2024安徽太和一模,19,★★☆)如图,C为⊙O上一点,直径AB = 26,∠ACB的平分线交⊙O于点D,交AB于点E,连接AD,BD.(M9224007)
(1)求BD的长.
(2)若AC = 10,求CD的长.
(1)求BD的长.
(2)若AC = 10,求CD的长.

答案:
解析:(1)如图,连接OD, 因为AB是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$。 因为CD是$\angle ACB$的平分线, 所以$\angle ACD=\angle BCD = 45^{\circ}$, 所以$\angle BOD = 2\angle BCD = 90^{\circ}$。 在$Rt\triangle BOD$中,$OB = OD=\frac{1}{2}AB = 13$, 所以$BD=\sqrt{2}OB = 13\sqrt{2}$。 (2)在$Rt\triangle ABC$中,$AC = 10$,$AB = 26$, 所以$BC=\sqrt{AB^{2}-AC^{2}} = 24$。 如图,过点B作$BM\perp CD$,垂足为M, 在$Rt\triangle BCM$中,$\angle BCM = 45^{\circ}$,$BC = 24$, 所以$CM = BM=\frac{\sqrt{2}}{2}BC = 12\sqrt{2}$。 在$Rt\triangle BDM$中,$BD = 13\sqrt{2}$,$BM = 12\sqrt{2}$, 所以$DM=\sqrt{BD^{2}-BM^{2}} = 5\sqrt{2}$, 所以$CD = CM + DM = 17\sqrt{2}$。
解析:(1)如图,连接OD, 因为AB是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$。 因为CD是$\angle ACB$的平分线, 所以$\angle ACD=\angle BCD = 45^{\circ}$, 所以$\angle BOD = 2\angle BCD = 90^{\circ}$。 在$Rt\triangle BOD$中,$OB = OD=\frac{1}{2}AB = 13$, 所以$BD=\sqrt{2}OB = 13\sqrt{2}$。 (2)在$Rt\triangle ABC$中,$AC = 10$,$AB = 26$, 所以$BC=\sqrt{AB^{2}-AC^{2}} = 24$。 如图,过点B作$BM\perp CD$,垂足为M, 在$Rt\triangle BCM$中,$\angle BCM = 45^{\circ}$,$BC = 24$, 所以$CM = BM=\frac{\sqrt{2}}{2}BC = 12\sqrt{2}$。 在$Rt\triangle BDM$中,$BD = 13\sqrt{2}$,$BM = 12\sqrt{2}$, 所以$DM=\sqrt{BD^{2}-BM^{2}} = 5\sqrt{2}$, 所以$CD = CM + DM = 17\sqrt{2}$。

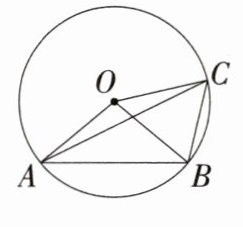
21.教材变式.P29T3(2023湖北武汉中考,20,)如图,OA,OB,OC都是⊙O的半径,∠ACB=2∠BAC.(M9224007)(1)求证:∠AOB=2∠BOC.(2)若AB=4,BC=$\sqrt 5$,求⊙O的半径

答案:
解析
(1)证明;
∵ ∠ACB= $\frac{1}{2}$ ∠AOB,∠BAC=$\frac{1}{2}$ ∠BOC,∠ACB=2∠BAC,
∴ ∠A0B=2∠B0C
(2)如图,过点O作半径OD⊥AB于点E,连接DB,
∴ AE=BE,∠DOB= $\frac{1}{2}$ ∠AOB,
∵ ∠A0B=2∠BOC,
∴ ∠DOB=∠BOC.
∴ BD=BC.
∵ AB=4,BC= $\sqrt{5}$
∴ BE=2,BD= $\sqrt{5}$ ,
∵ 在Rt△BDE中,∠DEB=90°,
∴ DE= $\sqrt{BD²−BE²}$ =1,
∵ 在Rtt△BOE中,∠OEB=90°,
∴ OB²=(OB−1)²+2²,解得OB= $\frac{5}{2}$ ,即⊙0的半径是 $\frac{5}{2}$
(1)证明;
∵ ∠ACB= $\frac{1}{2}$ ∠AOB,∠BAC=$\frac{1}{2}$ ∠BOC,∠ACB=2∠BAC,
∴ ∠A0B=2∠B0C
(2)如图,过点O作半径OD⊥AB于点E,连接DB,
∴ AE=BE,∠DOB= $\frac{1}{2}$ ∠AOB,
∵ ∠A0B=2∠BOC,
∴ ∠DOB=∠BOC.
∴ BD=BC.
∵ AB=4,BC= $\sqrt{5}$
∴ BE=2,BD= $\sqrt{5}$ ,
∵ 在Rt△BDE中,∠DEB=90°,
∴ DE= $\sqrt{BD²−BE²}$ =1,
∵ 在Rtt△BOE中,∠OEB=90°,
∴ OB²=(OB−1)²+2²,解得OB= $\frac{5}{2}$ ,即⊙0的半径是 $\frac{5}{2}$
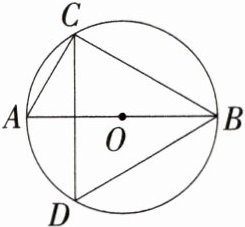
1.(2024四川宜宾中考)如图,AB是⊙O的直径,若∠CDB = 60°,则∠ABC的度数等于 ( )
A.30°
B.45°
C.60°
D.90°

A.30°
B.45°
C.60°
D.90°
答案:
A:因为AB是$\odot O$的直径,所以$\angle ACB = 90^{\circ}$,因为$\angle CDB = 60^{\circ}$,所以$\angle A=\angle CDB = 60^{\circ}$,所以$\angle ABC = 90^{\circ}-\angle A = 30^{\circ}$,故选A。
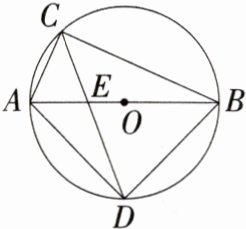
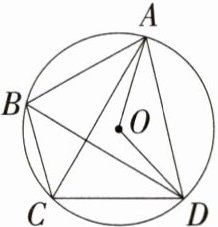
2.(2023浙江温州中考)如图,四边形ABCD内接于⊙O,BC//AD,AC⊥BD.若∠AOD = 120°,AD = $\sqrt{3}$,则∠CAO的度数与BC的长分别为 ( )
A.10°,1
B.10°,$\sqrt{2}$
C.15°,1
D.15°,$\sqrt{2}$

A.10°,1
B.10°,$\sqrt{2}$
C.15°,1
D.15°,$\sqrt{2}$
答案:
C:如图,连接OB,OC,因为$BC// AD$,所以$\angle DBC=\angle ADB$,所以$\widehat{AB}=\widehat{CD}$,所以$\angle AOB=\angle COD$,$\angle CAD=\angle BDA$,因为$DB\perp AC$,所以$\angle AED = 90^{\circ}$,所以$\angle CAD=\angle BDA = 45^{\circ}$,所以$\angle AOB = 2\angle ADB = 90^{\circ}$,$\angle COD = 2\angle CAD = 90^{\circ}$。因为$\angle AOD = 120^{\circ}$,所以$\angle BOC = 360^{\circ}-90^{\circ}-90^{\circ}-120^{\circ}=60^{\circ}$。因为$OB = OC$,所以$\triangle OBC$是等边三角形,所以$BC = OB$。因为$OA = OD$,$\angle AOD = 120^{\circ}$,所以$\angle OAD=\angle ODA = 30^{\circ}$,因为$AD=\sqrt{3}$,所以$OA = 1$,所以$BC = 1$,所以$\angle CAO=\angle CAD-\angle OAD = 45^{\circ}-30^{\circ}=15^{\circ}$。故选C。
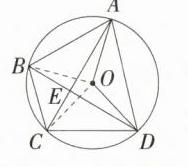
C:如图,连接OB,OC,因为$BC// AD$,所以$\angle DBC=\angle ADB$,所以$\widehat{AB}=\widehat{CD}$,所以$\angle AOB=\angle COD$,$\angle CAD=\angle BDA$,因为$DB\perp AC$,所以$\angle AED = 90^{\circ}$,所以$\angle CAD=\angle BDA = 45^{\circ}$,所以$\angle AOB = 2\angle ADB = 90^{\circ}$,$\angle COD = 2\angle CAD = 90^{\circ}$。因为$\angle AOD = 120^{\circ}$,所以$\angle BOC = 360^{\circ}-90^{\circ}-90^{\circ}-120^{\circ}=60^{\circ}$。因为$OB = OC$,所以$\triangle OBC$是等边三角形,所以$BC = OB$。因为$OA = OD$,$\angle AOD = 120^{\circ}$,所以$\angle OAD=\angle ODA = 30^{\circ}$,因为$AD=\sqrt{3}$,所以$OA = 1$,所以$BC = 1$,所以$\angle CAO=\angle CAD-\angle OAD = 45^{\circ}-30^{\circ}=15^{\circ}$。故选C。

查看更多完整答案,请扫码查看


