第14页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.下列关于确定一个圆的说法中,正确的是
( )
A.三个点一定能确定一个圆
B.以已知线段为半径只能确定一个圆
C.以已知线段为直径能确定一个圆
D.菱形的四个顶点能确定一个圆
( )
A.三个点一定能确定一个圆
B.以已知线段为半径只能确定一个圆
C.以已知线段为直径能确定一个圆
D.菱形的四个顶点能确定一个圆
答案:
C:当三个点在同一条直线上时不能确定圆,故A选项错误;以已知线段为半径能确定两个圆,这两个圆分别以线段的两个端点为圆心,故B选项错误;以已知线段为直径能确定一个圆,此时圆心为线段的中点,半径为线段长度的一半,故C选项正确;菱形的四个顶点不一定能确定一个圆,故D选项错误。故选C。
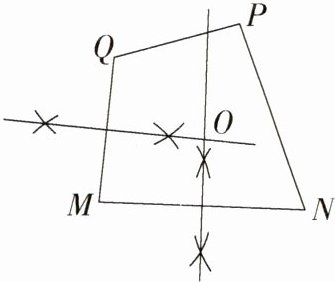
2.如图,小明为检验M、N、P、Q四点是否共圆,用尺规分别作了MN、MQ的垂直平分线,它们交于点O,则M、N、P、Q四点中,不一定在以O为圆心,OM长为半径的圆上的点是 ( )
A.M B.N
C.P D.Q
A.M B.N
C.P D.Q

答案:
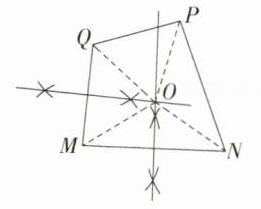
C:如图,连接OM、ON、OQ、OP,
∵MN、MQ的垂直平分线交于点O,
∴OM = ON = OQ,
∴M、N、Q在以点O为圆心,OM长为半径的圆上,
∵OP与OM的大小关系不能确定,
∴点P不一定在以O为圆心,OM长为半径的圆上. 故选C。
C:如图,连接OM、ON、OQ、OP,
∵MN、MQ的垂直平分线交于点O,
∴OM = ON = OQ,
∴M、N、Q在以点O为圆心,OM长为半径的圆上,
∵OP与OM的大小关系不能确定,
∴点P不一定在以O为圆心,OM长为半径的圆上. 故选C。

3.数形结合思想)(2023江苏宿迁泗洪二模)如图,在平面直角坐标系中,点A,B,C都在格点上,过A,
B,C三点作一圆弧,则圆心的坐标是________.
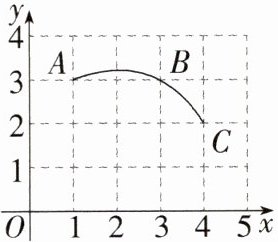
B,C三点作一圆弧,则圆心的坐标是________.

答案:
答案:(2, 1) 解析:如图,连接AB,BC,作线段AB的垂直平分线MN,BC的垂直平分线EF,MN与EF交于点Q,点Q即为圆心,则圆心的坐标是(2, 1)。
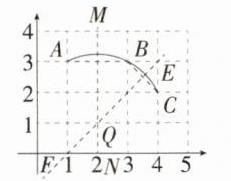
答案:(2, 1) 解析:如图,连接AB,BC,作线段AB的垂直平分线MN,BC的垂直平分线EF,MN与EF交于点Q,点Q即为圆心,则圆心的坐标是(2, 1)。

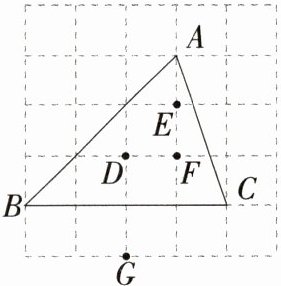
4.(2024广西柳州城中期中)如图所示的网格由边长相同的小正方形组成,点A,B,C,D,E,F,G 在小正方形的顶点上,则△ABC的外心是(M9224008) ( )
圆的确定
A.点D
B.点E
C.点F
D.点G
圆的确定

A.点D
B.点E
C.点F
D.点G
答案:
A:设题图中小正方形的边长为1,则AD = BD = CD = $\sqrt{1^{2}+2^{2}}=\sqrt{5}$,所以点D是△ABC的外心,故选A。
5.(2023安徽蚌埠蚌山期末)两直角边长分别为15 和20的直角三角形外接圆的半径为________.
答案:
答案:$\frac{25}{2}$
解析:由题意可求出该直角三角形的斜边长为$\sqrt{15^{2}+20^{2}} = 25$,
∵直角三角形的外心在其斜边中点处,
∴该直角三角形外接圆的半径为$\frac{25}{2}$。
∵直角三角形的外心在其斜边中点处,
∴该直角三角形外接圆的半径为$\frac{25}{2}$。
6.新考向.尺规作图)(2024山东滕州善国中学一模)
已知等腰△ABC,AB=AC=4,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆,并计算此外接圆的半径.(M9224011)
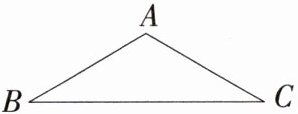
已知等腰△ABC,AB=AC=4,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆,并计算此外接圆的半径.(M9224011)

答案:
解析:作AB、AC的垂直平分线,交点O即为△ABC的外接圆的圆心,连接OA,以点O为圆心,OA长为半径画圆,则⊙O即为所求,如图。 连接OB.
∵AB = AC = 4,∠BAC = 120°,
∴∠BAO = 60°,
∴△ABO为等边三角形,
∴OA = AB = 4,
∴△ABC的外接圆的半径为4。
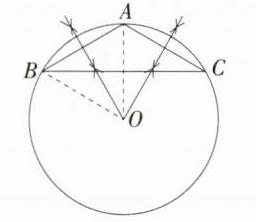
解析:作AB、AC的垂直平分线,交点O即为△ABC的外接圆的圆心,连接OA,以点O为圆心,OA长为半径画圆,则⊙O即为所求,如图。 连接OB.
∵AB = AC = 4,∠BAC = 120°,
∴∠BAO = 60°,
∴△ABO为等边三角形,
∴OA = AB = 4,
∴△ABC的外接圆的半径为4。

7.用反证法证明命题“三角形的三个内角中至少有一个不大于60o”有以下三个步骤:①因为∠A+∠B+∠C>60°+60°+60°=180°,这与三角形内角和为180°相矛盾;②所以一个三角形的三个内角中至少有一个不大于60°;③假设三角形的三个内角∠A、∠B、∠C都大于60°.这三个步骤的正确顺序为 ( )
A.③①②
B.②③①
C.①③②
D.①②③
A.③①②
B.②③①
C.①③②
D.①②③
答案:
A:用反证法证明命题的步骤是反设、推理、结论,所以正确的顺序是③①②。
8.用反证法证明:一个圆只有一个圆心.
答案:
证明:如图,假设⊙O有两个圆心,为O和O',在圆内任作一弦AB,设弦AB的中点为P,连接OP,O'P,则OP⊥AB,O'P⊥AB,此时过直线AB上一点P,同时有两条直线OP,O'P垂直于AB,与在同一平面内,过一点有且只有一条直线垂直于已知直线矛盾,故一个圆只有一个圆心。
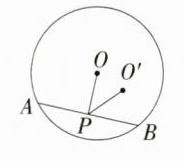
证明:如图,假设⊙O有两个圆心,为O和O',在圆内任作一弦AB,设弦AB的中点为P,连接OP,O'P,则OP⊥AB,O'P⊥AB,此时过直线AB上一点P,同时有两条直线OP,O'P垂直于AB,与在同一平面内,过一点有且只有一条直线垂直于已知直线矛盾,故一个圆只有一个圆心。

查看更多完整答案,请扫码查看


