《2025年5年中考3年模拟九年级数学下册沪科版》

1.如图，足球运动员在球门AB前沿直线l横向带球准备射门，不考虑其他因素，关于C、D两处射门进球的可能性，下列说法正确的是（ ）

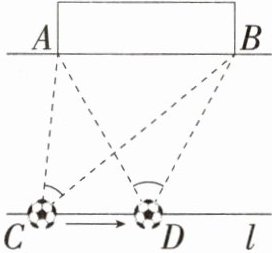
A.在C处射门进球的可能性大
B.在D处射门进球的可能性大
C.在C、D两处射门进球的可能性一样大
D.无法判断在C、D两处哪处射门进球的可能性更大

答案： 1. B 因为点 D 距离球门 AB 的中心比较近，所以∠ADB 大于∠ACB，所以在 D 处射门进球的可能性大。

2.足球射门，不考虑其他因素，仅考虑射门点到球门AB的张角大小时，张角越大，射门点越好.如图，在正方形网格中，点A，B，C，D，E均在格点上，球员带球沿CD方向进攻，最好的射门点在（ ）

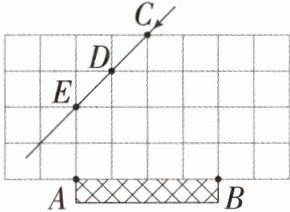
A.点C处
B.点D处或点E处
C.线段DE(异于端点）上
D.线段CD(异于端点）上

答案：
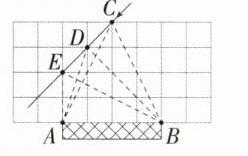
2. C 如图，连接 BC，AC，BD，AD，AE，BE，
∵∠EAB = ∠EDB = 90°，
∴ A，B，D，E 四点共圆，则∠ADB = ∠AEB，在弦的同侧，同弦对应的圆内角大于圆周角，圆外角小于圆周角，因而球员带球沿 CD 方向进攻时，最好的射门点在 DE（异于端点）上，故选 C。

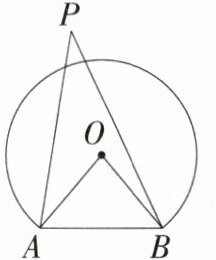
3.如图，海边立有两座灯塔A、B，暗礁分布在经过A、B两点的弓形(弓形的弧是⊙O的一部分)区域内部(不包括弓形边缘)，∠AOB = 80°.为了避免触礁，轮船P与A、B的张角∠APB(P始终在AB上方)的最大度数为______.

答案： 3. 答案 40° 解析 由题意知，为了避免触礁，当 P 点在圆上，不进入经过 A、B 两点的弓形区域内部时，轮船 P 与 A、B 的张角∠APB 最大，为∠AOB 的一半，即∠APB 的最大度数为 40°。

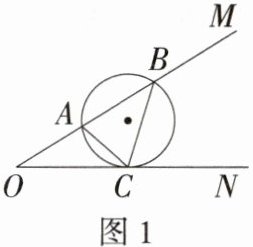
4.(2023广西北海二模节选，23，★★☆)【数学理解】德国数学家米勒曾提出最大视角问题，对该问题的一般描述是：如图1，已知点A，B是∠MON的边OM上的两个定点，C是ON边上的一个动点，当且仅当△ABC的外接圆与ON边相切于点C时，∠ACB最大.
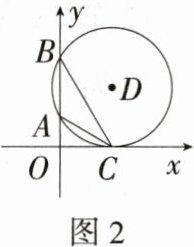
【问题解决】如图2，已知点A，B的坐标分别是(0，1)，(0，3)，C是x轴正半轴上的一动点，当△ABC的外接圆⊙D与x轴相切于点C时，∠ACB最大.当∠ACB最大时，求点C的坐标.

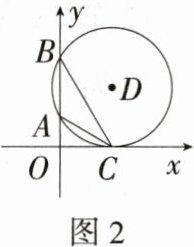
答案：
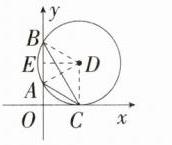
4. 解析 如图，连接 DC，DA，DB，过点 D 作 DE⊥AB 交 y 轴于点 E，
∵AE = BE = $\frac{1}{2}$AB，∠DEO = 90°

∵⊙D 与 x 轴相切于点 C，
∴DC⊥x 轴，
∴∠DEO = ∠DCO = ∠COE = 90°。
∴四边形 COED 是矩形，
∴CD = OE，DE = OC，
∵A(0,1)，B(0,3)，
∴AB = 2，OA = 1，
∴AE = BE = 1，
∴BD = CD = OE = AE + OA = 2，
∴OC = DE = $\sqrt{BD^{2}-BE^{2}}$ = $\sqrt{2^{2}-1^{2}}$ = $\sqrt{3}$，
∴C($\sqrt{3}$,0)。