第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
18.(6分)如图,⊙O是正方形ABCD的外接圆,MN是⊙O的弦,且经过正方形ABCD的边AD,CD的中点E,F,若MN = 12$\sqrt{3}$,求⊙O的半径长.
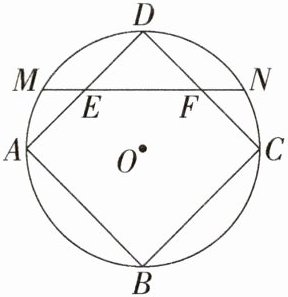

答案:
解析 如图,连接OE,OF,OD,OM,ON,OD交MN于点G,
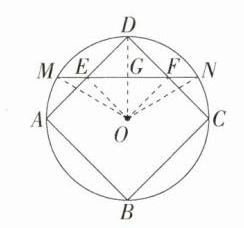
∵E,F分别为DA,DC的中点,
∴OE⊥AD,OF⊥CD,DE = $\frac{1}{2}AD$,DF = $\frac{1}{2}DC$,
∵四边形ABCD为正方形,
∴∠ADC = 90°,AD = CD,
∴四边形OEDF是矩形,DE = DF,
∴四边形OEDF是正方形,
∴OG = $\frac{1}{2}OD$,OG⊥MN,
∴MG = $\frac{1}{2}MN = 6\sqrt{3}$。设⊙O的半径为r,由勾股定理,得OG² + MG² = OM²,即$(\frac{1}{2}r)^{2}+(6\sqrt{3})^{2}=r^{2}$,解得r = 12(负值已舍去),即⊙O的半径长为12。
解析 如图,连接OE,OF,OD,OM,ON,OD交MN于点G,

∵E,F分别为DA,DC的中点,
∴OE⊥AD,OF⊥CD,DE = $\frac{1}{2}AD$,DF = $\frac{1}{2}DC$,
∵四边形ABCD为正方形,
∴∠ADC = 90°,AD = CD,
∴四边形OEDF是矩形,DE = DF,
∴四边形OEDF是正方形,
∴OG = $\frac{1}{2}OD$,OG⊥MN,
∴MG = $\frac{1}{2}MN = 6\sqrt{3}$。设⊙O的半径为r,由勾股定理,得OG² + MG² = OM²,即$(\frac{1}{2}r)^{2}+(6\sqrt{3})^{2}=r^{2}$,解得r = 12(负值已舍去),即⊙O的半径长为12。
19.(安徽常考·网格作图题)(2023安徽蚌埠龙子湖二模)(6分)如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后的△A₁B₁C;平移△ABC,若A的对应点A₂的坐标为(0,-4),画出平移后的△A₂B₂C₂.
(2)若将△A₁B₁C绕某一点P旋转可以得到△A₂B₂C₂,请直接写出旋转中心P点的坐标.
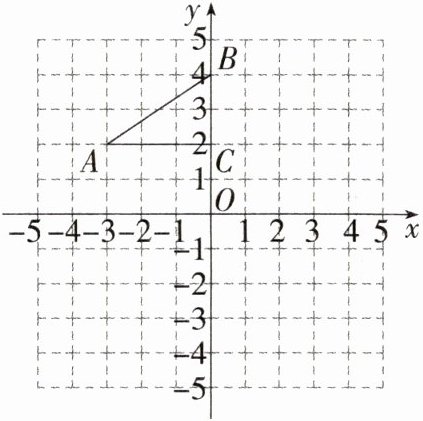
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后的△A₁B₁C;平移△ABC,若A的对应点A₂的坐标为(0,-4),画出平移后的△A₂B₂C₂.
(2)若将△A₁B₁C绕某一点P旋转可以得到△A₂B₂C₂,请直接写出旋转中心P点的坐标.

答案:
解析 (1)如图,△A₁B₁C即为所求,△A₂B₂C₂即为所求。
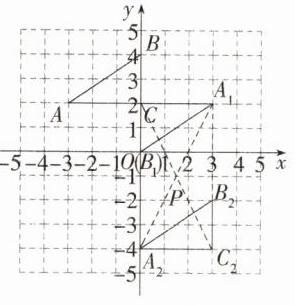
(2)如图,P点的坐标为$(\frac{3}{2}, - 1)$。
解析 (1)如图,△A₁B₁C即为所求,△A₂B₂C₂即为所求。

(2)如图,P点的坐标为$(\frac{3}{2}, - 1)$。
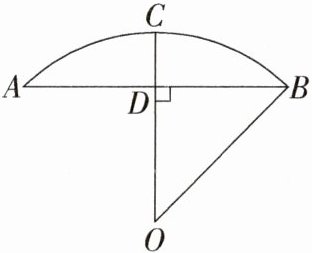
20.(跨历史·石拱桥)(2022湖北宜昌中考)(6分)石拱桥是我国古代人民勤劳和智慧的结晶,隋代建造的赵州桥距今约有1 400年历史,是我国古代石拱桥的代表.如图所示的是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为$\overset{\frown}{AB}$,桥的跨度(弧所对的弦长)AB = 26 m,设$\overset{\frown}{AB}$所在圆的圆心为O,半径OC⊥AB,垂足为D,拱高(弧的中点到弦的距离)CD = 5 m,连接OB.
(1)直接判断AD与BD的数量关系.
(2)求这座石拱桥主桥拱的半径(精确到1 m).
(1)直接判断AD与BD的数量关系.
(2)求这座石拱桥主桥拱的半径(精确到1 m).

答案:
解析 (1)AD = BD。
(2)设主桥拱的半径为R m,
∵AB = 26 m,CD = 5 m,
∴BD = $\frac{1}{2}AB=\frac{1}{2}×26 = 13$ m,OD = OC - CD = (R - 5) m,在Rt△OBD中,由勾股定理,得OB² = BD² + OD²,即R² = 13² + (R - 5)², 解得R = 19.4,
∴R≈19, 因此,这座石拱桥的主桥拱的半径约为19 m。
∵AB = 26 m,CD = 5 m,
∴BD = $\frac{1}{2}AB=\frac{1}{2}×26 = 13$ m,OD = OC - CD = (R - 5) m,在Rt△OBD中,由勾股定理,得OB² = BD² + OD²,即R² = 13² + (R - 5)², 解得R = 19.4,
∴R≈19, 因此,这座石拱桥的主桥拱的半径约为19 m。
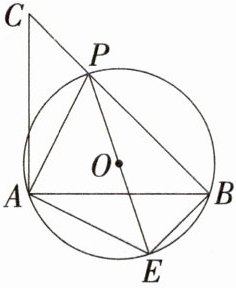
21.(2023浙江杭州中泰中学月考)(6分)如图,已知等腰直角△ABC,P是斜边BC上一点(不与B,C重合),PE是△ABP的外接圆⊙O的直径.
(1)求证:△APE是等腰直角三角形.
(2)若PC = 2,PB = 4,求PE的长.
(1)求证:△APE是等腰直角三角形.
(2)若PC = 2,PB = 4,求PE的长.

答案:
解析 (1)证明:
∵AB = AC,∠BAC = 90°,
∴∠C = ∠ABC = 45°,
∴∠AEP = ∠ABP = 45°,
∵PE是直径,
∴∠PAE = 90°,
∴∠APE = ∠AEP = 45°,
∴AP = AE,
∴△PAE是等腰直角三角形。 (2)
∵∠CAB = ∠PAE = 90°,
∴∠CAP = ∠BAE, 又AC = AB,AP = AE,
∴△CAP≌△BAE(SAS),
∴PC = EB, 又
∵∠PBE = 90°,
∴PE² = PB² + BE² = PB² + PC²,
∴PE² = 16 + 4 = 20,
∴PE = $2\sqrt{5}$。
∵AB = AC,∠BAC = 90°,
∴∠C = ∠ABC = 45°,
∴∠AEP = ∠ABP = 45°,
∵PE是直径,
∴∠PAE = 90°,
∴∠APE = ∠AEP = 45°,
∴AP = AE,
∴△PAE是等腰直角三角形。 (2)
∵∠CAB = ∠PAE = 90°,
∴∠CAP = ∠BAE, 又AC = AB,AP = AE,
∴△CAP≌△BAE(SAS),
∴PC = EB, 又
∵∠PBE = 90°,
∴PE² = PB² + BE² = PB² + PC²,
∴PE² = 16 + 4 = 20,
∴PE = $2\sqrt{5}$。
查看更多完整答案,请扫码查看


