第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
1.(2024 河南舞阳期末)定义:圆中有一公共端点的两条弦组成的折线称为圆的一条折弦. 如图,AB和BC组成圆的一条折弦,AB>BC,M是$\overset{\frown}{ABC}$的中点,MF⊥AB于F,则下列结论一定成立的是( )
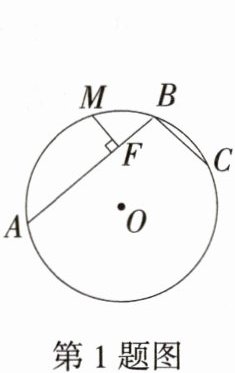
A.MF = BF
B.∠ABC = 90°
C.AF = FB + BC
D.AB = 2BC

A.MF = BF
B.∠ABC = 90°
C.AF = FB + BC
D.AB = 2BC
答案:
**C** 如图,在 AB 上截取 AD = BC,连接 AM,CM,DM,BM,
∵ M 是 $\overset{\frown}{ABC}$ 的中点,
∴ $\overset{\frown}{AM}=\overset{\frown}{CM}$,
∴ AM = CM。又
∵ ∠MAD = ∠MCB,
∴ △MAD ≌ △MCB(SAS),
∴ MD = BM,
∵ MF ⊥ AB,
∴ DF = BF,
∴ AF = AD + DF = FB + BC,故 C 中结论成立,根据题目给出的条件不能说明选项 A、B、D 中结论一定成立,故选 C

**C** 如图,在 AB 上截取 AD = BC,连接 AM,CM,DM,BM,
∵ M 是 $\overset{\frown}{ABC}$ 的中点,
∴ $\overset{\frown}{AM}=\overset{\frown}{CM}$,
∴ AM = CM。又
∵ ∠MAD = ∠MCB,
∴ △MAD ≌ △MCB(SAS),
∴ MD = BM,
∵ MF ⊥ AB,
∴ DF = BF,
∴ AF = AD + DF = FB + BC,故 C 中结论成立,根据题目给出的条件不能说明选项 A、B、D 中结论一定成立,故选 C

2.(新考向·规律探究试题)(2024 广东韶关模拟)如图,四边形ABCD是正方形,曲线$DA_1B_1C_1D_1A_2B_2\cdots$叫做“正方形的渐开线”,其中$\overset{\frown}{DA_1}$的圆心为点A,半径为AD;$\overset{\frown}{A_1B_1}$的圆心为点B,半径为$BA_1$;$\overset{\frown}{B_1C_1}$的圆心为点C,半径为$CB_1$;$\overset{\frown}{C_1D_1}$的圆心为点D,半径为$DC_1$;…….$\overset{\frown}{DA_1}$,$\overset{\frown}{A_1B_1}$,$\overset{\frown}{B_1C_1}$,$\overset{\frown}{C_1D_1}$,…的圆心按A,B,C,D依次循环,当AB = 1时,$\overset{\frown}{A_{2024}B_{2024}}$的长是__________.
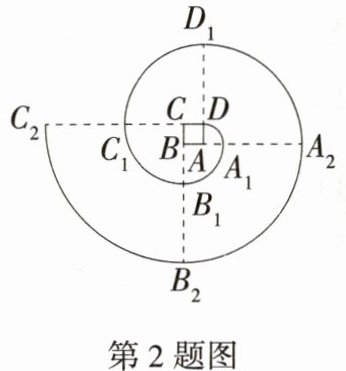

答案:
**答案**:4 047π
**解析**:由题图可知,曲线 DA₁B₁C₁D₁A₂B₂…是由一段段 90°的弧组成的,AA₁ = AD = 1,BB₁ = BA₁ = BA + AA₁ = 1 + 1 = 2,CC₁ = CB + BB₁ = 1 + 2 = 3,DD₁ = DC + CC₁ = 1 + 3 = 4,AA₂ = AD + DD₁ = 1 + 4 = 5,……,以此类推,每一段弧的半径等于前一段弧半径加 1,AAₙ = 4(n - 1) + 1,BAₙ = 4(n - 1) + 2,
∴ BA₂₀₂₄ = 4×(2 024 - 1) + 2 = 8 094,
∴ $\overset{\frown}{A_{2024}B_{2024}}$ 的长 = $\frac{90}{180}$×8 094π = 4 047π。
∴ BA₂₀₂₄ = 4×(2 024 - 1) + 2 = 8 094,
∴ $\overset{\frown}{A_{2024}B_{2024}}$ 的长 = $\frac{90}{180}$×8 094π = 4 047π。
3.对于实数a、b,定义两种新运算“*”和“⊕”:$a*b=a + rb$,$a\oplus b=ra + b$(其中a、b分别为圆心在平面直角坐标系中的横、纵坐标,r为圆的半径). 在平面直角坐标系中,⊙P的半径r = 5,且$a*b = 23$,$a\oplus b = 19$,则坐标原点在⊙P______(填“外”“内”或“上”),⊙P与x轴的位置关系是________.
答案:
**答案**:上;相交
**解析**:由题意,得 $\begin{cases}a + 5b = 23 \\5a + b = 19\end{cases}$,解得 $\begin{cases}a = 3 \\b = 4\end{cases}$,
∴ 圆心 P 的坐标为(3, 4),
∴ 圆心到坐标原点的距离为 $\sqrt{3^{2}+4^{2}}$ = 5,
∴ 坐标原点在⊙P 上。
∵ P 到 x 轴的距离等于 4,4 < 5,
∴ ⊙P 与 x 轴相交。
∴ 圆心 P 的坐标为(3, 4),
∴ 圆心到坐标原点的距离为 $\sqrt{3^{2}+4^{2}}$ = 5,
∴ 坐标原点在⊙P 上。
∵ P 到 x 轴的距离等于 4,4 < 5,
∴ ⊙P 与 x 轴相交。
4.如图①,在等腰△ABC中,AB = AC,当顶角∠A的大小确定时,它的对边BC与邻边AB(或AC)的比值也就确定了,我们把这个比值记作T(A),即$T(A)=\frac{\angle A的对边}{\angle A的邻边}=\frac{BC}{AB}(或\frac{BC}{AC})$,如:当∠A = 60°时,$T(60°)=1$.
(1)理解巩固:$T(90°)=$_______,$T(120°)=$_______,T(A)的值的范围是__________.
(2)学以致用:如图②,圆锥的母线长为9,底面圆的直径PQ = 8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长.(精确到0.1. 参考数据:$T(160°)\approx1.97$,$T(80°)\approx1.29$,$T(40°)\approx0.68$)

(1)理解巩固:$T(90°)=$_______,$T(120°)=$_______,T(A)的值的范围是__________.
(2)学以致用:如图②,圆锥的母线长为9,底面圆的直径PQ = 8,一只蚂蚁从点P沿着圆锥的侧面爬行到点Q,求蚂蚁爬行的最短路径长.(精确到0.1. 参考数据:$T(160°)\approx1.97$,$T(80°)\approx1.29$,$T(40°)\approx0.68$)

答案:
**解析**: (1)如图 1,∠A = 90°,AB = AC,则 $\frac{BC}{AB}$ = $\sqrt{2}$,
∴ T(90°) = $\sqrt{2}$。 如图 2,∠BAC = 120°,AB = AC,过 A 作 AD ⊥ BC 于 D,则 ∠BAD = 60°,
∴ BD = $\frac{\sqrt{3}}{2}$AB,
∴ BC = $\sqrt{3}$AB,
∴ $\frac{BC}{AB}$ = $\sqrt{3}$,即 T(120°) = $\sqrt{3}$。
∵ AB - AC < BC < AB + AC,
∴ 0 < T(A) < 2。 (2)
∵ 圆锥的底面圆的直径 PQ = 8,
∴ 圆锥的底面圆的周长为 8π,
∴ 圆锥的侧面展开图(扇形)的弧长为 8π, 设扇形的圆心角的度数为 n°, 则 $\frac{nπ×9}{180}$ = 8π,解得 n = 160,
∵ 160°÷2 = 80°,T(80°) ≈ 1.29,
∴ 蚂蚁爬行的最短路径长为 1.29×9 ≈ 11.6。
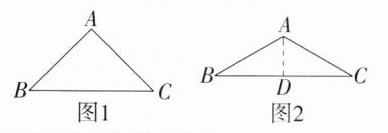
**解析**: (1)如图 1,∠A = 90°,AB = AC,则 $\frac{BC}{AB}$ = $\sqrt{2}$,
∴ T(90°) = $\sqrt{2}$。 如图 2,∠BAC = 120°,AB = AC,过 A 作 AD ⊥ BC 于 D,则 ∠BAD = 60°,
∴ BD = $\frac{\sqrt{3}}{2}$AB,
∴ BC = $\sqrt{3}$AB,
∴ $\frac{BC}{AB}$ = $\sqrt{3}$,即 T(120°) = $\sqrt{3}$。
∵ AB - AC < BC < AB + AC,
∴ 0 < T(A) < 2。 (2)
∵ 圆锥的底面圆的直径 PQ = 8,
∴ 圆锥的底面圆的周长为 8π,
∴ 圆锥的侧面展开图(扇形)的弧长为 8π, 设扇形的圆心角的度数为 n°, 则 $\frac{nπ×9}{180}$ = 8π,解得 n = 160,
∵ 160°÷2 = 80°,T(80°) ≈ 1.29,
∴ 蚂蚁爬行的最短路径长为 1.29×9 ≈ 11.6。

查看更多完整答案,请扫码查看


