《2025年5年中考3年模拟九年级数学下册沪科版》

1.下列说法中,不正确的是 （ ）
A.圆既是轴对称图形又是中心对称图形
B.圆有无数条对称轴
C.圆的每一条直径都是它的对称轴
D.圆的对称中心是它的圆心

答案： C：圆的直径所在的直线是圆的对称轴，而直径是线段，故不能说直径是圆的对称轴，C中说法错误。

2.(2024河北石家庄模拟)如图,CD是⊙O的直径,AB是弦,CD⊥AB,垂足为E,连接AO,则下列结论不一定正确的是(M9224006) （ ）

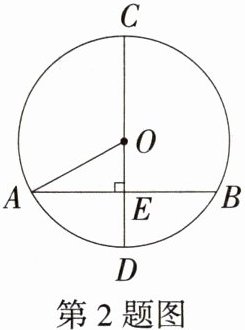
A.AE=BE
B.OE=DE
C.AO=CO
D.$\overset{\frown}{AD}=\overset{\frown}{BD}$

答案： B：因为CD是⊙O的直径，AB是弦，CD⊥AB，所以AE = BE，$\overset{\frown}{AD}=\overset{\frown}{BD}$；又因为⊙O的半径都相等，所以AO = CO，根据已知条件不能得出OE = DE，故选B。

3.(2024广西浦北期末)如图,⊙O的半径为13,弦AB=24,OC⊥AB于点C,则OC的长为 ( )

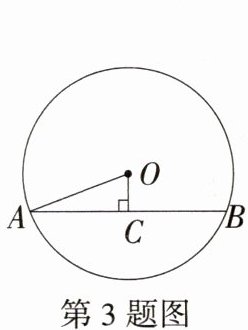
A.10
B.6
C.5
D.12

答案： C：因为OC⊥AB，AB = 24，所以AC = BC=$\frac{1}{2}AB=\frac{1}{2}\times24 = 12$；因为⊙O的半径为13，所以OA = 13；在Rt△OAC中，$OC=\sqrt{OA^{2}-AC^{2}}=\sqrt{13^{2}-12^{2}} = 5$，故选C。

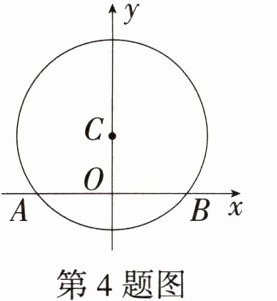
4.新独家原创 如图,在平面直角坐标系xOy中,⊙C的半径为5,圆心C的坐标为(0,3),则AB的长为________.

答案： 答案：8 解析：因为AB⊥CO，所以OA = OB。连接AC（图略），因为⊙C的半径为5，所以AC = 5；因为点C的坐标为(0, 3)，所以OC = 3；在Rt△OAC中，根据勾股定理，得$AO^{2}=AC^{2}-OC^{2}=25 - 9 = 16$，所以AO = 4，所以AB = 2AO = 8。

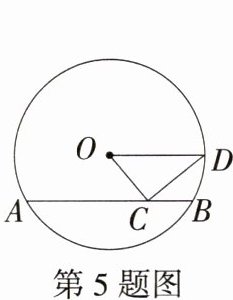
5.如图,在⊙O中,弦AB=4,点C在AB上移动,连接OC,过点C作CD⊥OC,交⊙O于点D,连接OD,则CD长的最大值为________.(M9224006)

答案： 答案：2 解析：因为CD⊥OC，所以∠DCO = 90°，所以$CD=\sqrt{OD^{2}-OC^{2}}$；因为OD是⊙O的半径，所以OD的长为定值，所以当OC的长最小时，CD的长最大。当OC⊥AB时，OC的长最小，此时$CD = CB=\frac{1}{2}AB = 2$，即CD长的最大值为2。

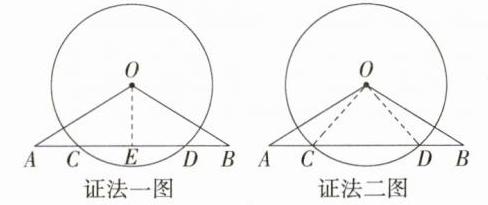
6.一题多解 教材变式·P17T2 如图,在△OAB中,⊙O交AB于点C、D,且AC=BD,求证:OA=OB.

答案：
证明\n【证法一】过点O作OE⊥AB于点E，如图。因为OE⊥CD，所以CE = DE；因为AC = BD，所以AC + CE = BD + DE，即AE = BE，所以点O在线段AB的垂直平分线上，所以OA = OB。\n【证法二】连接OC，OD，如图。因为OC = OD，所以∠OCD = ∠ODC，所以∠ACO = ∠BDO；又因为AC = BD，所以△ACO≌△BDO，所以OA = OB。

7.跨历史·遗址 安徽名胜·曹操运兵道 曹操运兵道又称曹操藏兵道,位于安徽省亳州市老城内主要街道下,目前已发现八千余米,它远远超过地面上保留的一座完整古老城池的价值,被誉为“地下长城”.如图,已知运兵道的宽度为0.8 m(AB=0.8 m),运兵道的高度为1.8 m(EG=1.8 m),其中侧墙的高度为1.6 m(AD=1.6 m),已知EG过点O,且EG⊥AB,垂足为F,求$\overset{\frown}{AB}$所在⊙O的半径.(M9224006)

答案： 解析：由题意得EF = 1.8 - 1.6 = 0.2(m)，OF⊥AB；因为AB = 0.8 m，所以$AF=\frac{1}{2}AB = 0.4 m$。设$\overset{\frown}{AB}$所在⊙O的半径为r m，则OF = (r - 0.2)m；在Rt△AOF中，由勾股定理，得$OA^{2}=AF^{2}+OF^{2}$，即$r^{2}=0.4^{2}+(r - 0.2)^{2}$，解得r = 0.5。 答：$\overset{\frown}{AB}$所在⊙O的半径为0.5 m。 方法归纳：在运用垂径定理时，常构造以半径、半弦长、弦心距为三边长的直角三角形，利用勾股定理求解。